前几天 openai 隆重推出 gpt-oss,模型的 MoE 部分采用了 MXFP4 格式让人震惊,这大大减少了对内存的依赖。
什么是 MXFP4
FP4在Open Compute Project, 2023.中有所定义
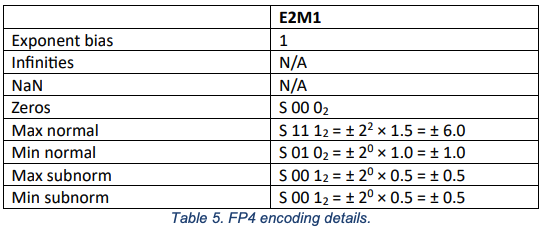
- FP4 支持 subnormals 非正规数。
- FP4 中没有为无穷大(Inf)或非数字(NaN)保留编码。
- 必须支持将值转换为 FP4 时的“roundTiesToEven”(偶数舍入)舍入模式。
- 在将值转换为 FP4 时,如果值在舍入后超出了 FP4 的可表示范围,实现必须支持将值钳制(饱和)到 FP4 的最大幅度,同时保留符号。
- 在将值转换为 FP4 时,如果值在舍入后小于 FP4 的最小非正规数幅度,实现必须将该值转换为零。
非正规数(Subnormal Numbers,也称为次正规数或非规格化数)是浮点数表示中的一种特殊形式,用于表示那些非常接近零但小于正规数(Normalized Numbers)最小值的数。它们的引入是为了填补浮点数表示范围中接近零的部分,从而避免在数值计算中因数值过小而直接变为零,从而提高数值精度。
对于一个标准的浮点数(如 IEEE 754 格式),其表示形式为:
\(Value = (-1)^{sign} * 1.mantissa * 2^{exponent}\)
其中,尾数部分通常被规范化为一个介于 1 和 2 之间的数(即形式为 \(1.mantissa\))。这种表示方式称为正规数。
当指数部分的值为最小可能值时(即所有指数位都为 0),浮点数不再使用隐含的前导 1,而是直接使用尾数部分的值。这种表示方式称为非正规数,其形式为:
\(Value = (-1)^{sign} * 0.mantissa * 2^{exponent\_bias}\)
其中,\(exponent\_bias\) 是一个偏移量,用于调整指数的实际值。对于非正规数,指数部分的值固定为最小可能值(通常是偏移量减去 1)。
非正规数的优缺点
- 优点:
- 提高了接近零的数值的精度。
- 使得浮点数的表示范围更加连续。
- 缺点:
- 非正规数的计算速度通常比正规数慢,因为它们需要特殊的处理逻辑。
- 在某些应用中,非正规数可能会导致性能问题,因为它们需要额外的计算开销。
MXFP4 is a micro-scaling block floating-point format, hence the name MXFP4 rather than just FP4.
这种 micro-scaling function 非常重要,因为 FP4 本身并不能提供很高的分辨率。它仅用四位(一位表示符号位,两位表示指数位,一位表示尾数)就可以表示 16 个不同的值:八个正值和八个负值。相比之下,BF16 可以表示 65,536 个值。openai_mxfp4
MXFP4 不是将缩放因子应用于整个张量,而是将其应用于张量内的较小块,从而允许值之间具有更大的粒度。
MXFP4 很重要,因为权重越小,运行模型所需的 VRAM、内存带宽以及潜在的计算能力就越少。换句话说,MXFP4 让 genAI 的成本大大降低。
Conversion from Vector of Scalar Elements to MX-compliant Format

A power-of-two is a number of the form \(2^n\) where n is a positive integer, negative integer, or zero.
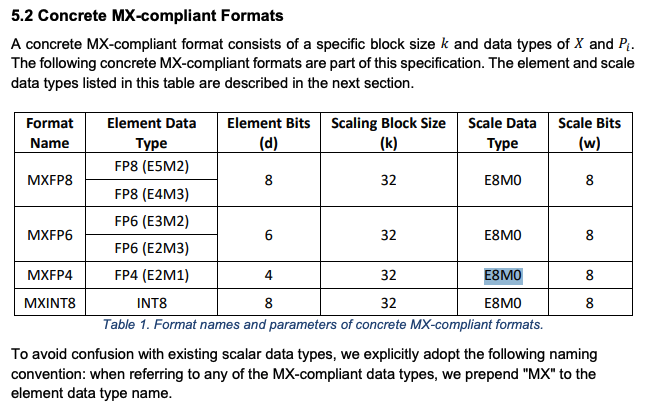
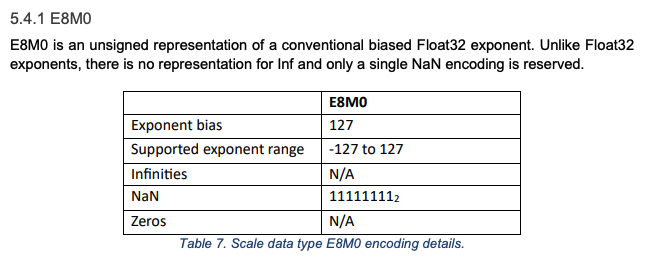

这种计算方式很有意思,应该能减少一些scale乘法,之后可以评估一下有没有收益
NVFP4
Introducing NVFP4 for Efficient and Accurate Low-Precision Inference
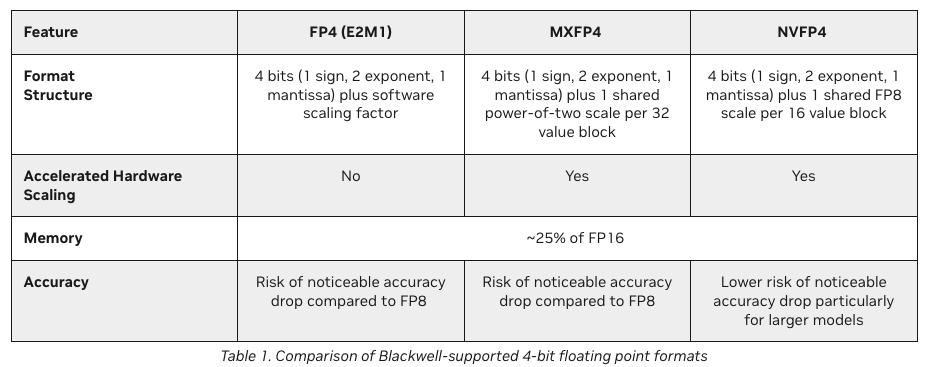
整体感受,如果能保住效果,MXFP4更加简洁高效,否则就要考虑NVFP4。虽然 MXFP4 远优于标准 FP4,但它并非灵丹妙药。Nvidia 认为, 与 FP8 相比,该数据类型的性能仍可能下降,部分原因是其 32 位值块大小不够精细。为了解决这个问题,这家 GPU 巨头推出了自己的微缩放数据类型 NVFP4,旨在通过使用 16 位值块和 FP8 缩放因子来提高质量。
MXFP4 isn’t just “smaller numbers” it’s the bridge between impossible and possible in AI. By packing more intelligence into fewer bits, and by making sure anyone can train and deploy powerful models, MXFP4 signals the democratization of AI is truly here. 来源
Training LLMs with MXFP4
建立在 IEEE 浮点数的基础上,通过向基本 IEEE 浮点数添加分组缩放
此缩放允许 MXFP 张量采用更广泛的值范围,而不会显著增加总比特率,但需要注意的是,组中的条目应大致具有相同的数量级才能使缩放有用。实际上,随着基本数据类型比特率的降低,MX 缩放变得更加重要。
FP8 E4M3 的动态范围为 \(448/2^{−9}=2.3×10^6\) ,而 FP4 的动态范围为 \(6/0.5=12\) 。MX 缩放使 MXFP4 能够跨块表示更大范围的值。
使用随机舍入 (SR) 和随机 Hadamard 变换 (RHT)。
- 随机舍入stochastic rounding (SR)可产生无偏梯度估计
- SR 增加的开销不到 10%
- random Hadamard transform (RHT) 可降低 SR 的方差并降低因下溢而丢失梯度信息的可能性。
开始实践
OpenAI 的 gpt-oss 模型是首批利用 MXFP4 的主流 LLM 之一。oai_gpt-oss_model_card
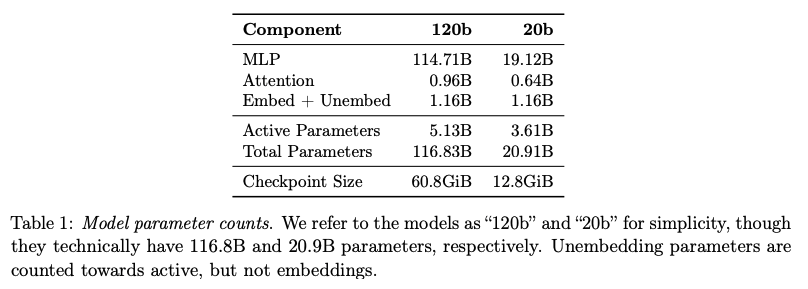
下载模型:https://huggingface.co/openai/gpt-oss-20b/tree/main
sglang的 Benchmark
1 | w_bf16 = dequant_mxfp4(w_block=w_blocks, w_scale=w_scales, out_dtype=torch.bfloat16) |
sglang里面是将mxfp4 dequant到 bf16之后计算的
sglang小结论:
gpt-oss 的 MoE weights 量化成了MXFP4 格式,4.25 bits per parameter(因为每32个为一个block,有一个E8M0的scale)
MoE 权重占总参数数量的 90% 以上。
- GPT-OSS-120B:每个 MoE 模块包含 128 个专家,每个 token 激活 4 个专家。
- GPT-OSS-20B:每个 MoE 模块包含 32 个专家,每个 token 激活 4 个专家。
- sglang的MXFP4推理是将mxfp4 dequant到
bf16之后计算的,转换方式位于
class MXFP4QuantizeUtil,采用了一些位运算和查表的方式。
后续可以看看写专门针对 MXFP4 的算子?不过手里也没有 Blackwell 的机器,难以推进,不过可以考虑转成fp8来加速。但是MoE的计算比较少,可能没有太大的意义。


