Zhao Dongyu's Blog

A life which is unexamined is not worth living.

0%

113_tensorflow实现量化softmax算子

Posted on In
Symbols count in article: 3k Reading time ≈ 3 mins.

研究了一下 tensorflow 实现 int8 量化的 softmax 算子

以这个算子为例：

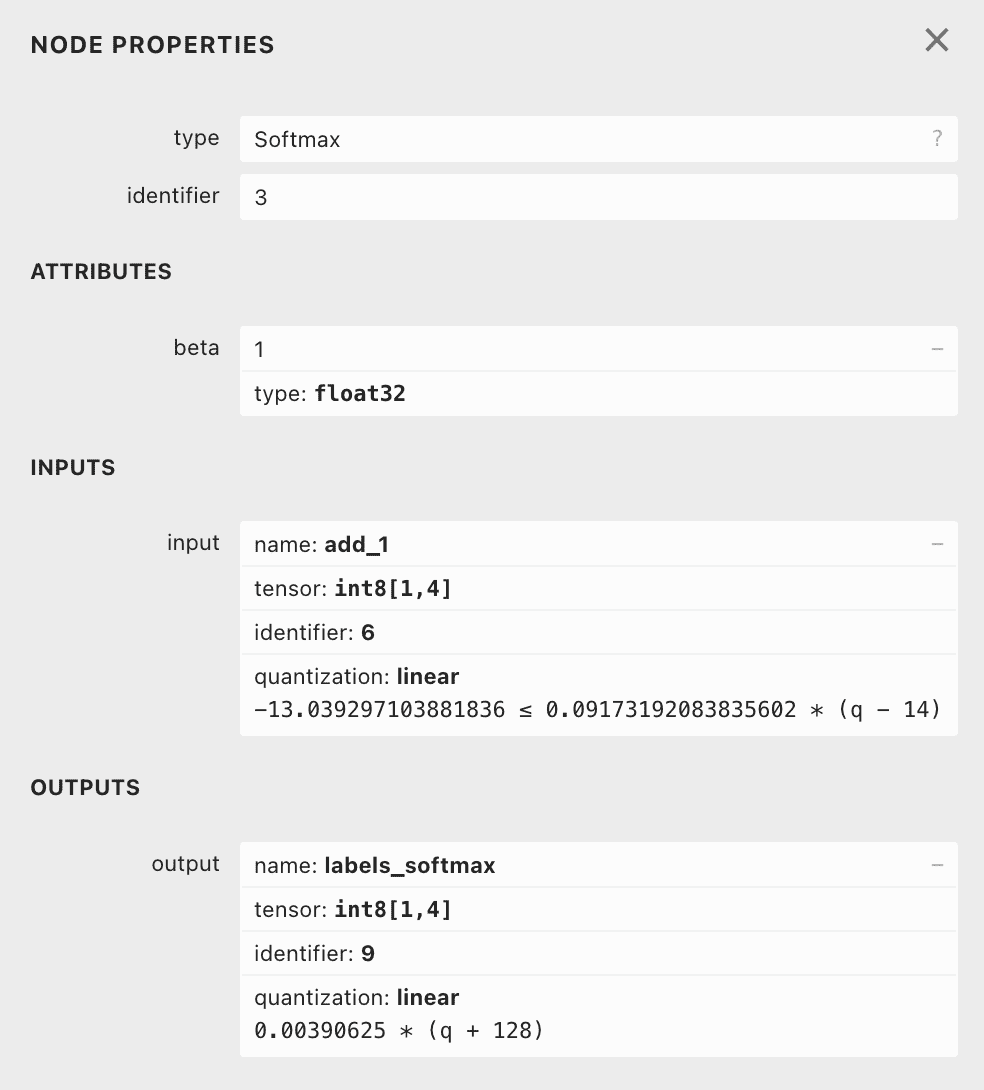
首先要计算一些参数

在 CalculateSoftmaxParams 函数中，

先确保了2个参数： 

1
2
TF_LITE_ENSURE_EQ(context, output->params.zero_point, -128);
TF_LITE_ENSURE(context, output->params.scale == 1.f / 256);
看来量化的softmax算子的输出 tensor 的 scale 和 zero point 是固定的。

然后是函数 

1
2
3
4
tflite::PreprocessSoftmaxScaling(
    static_cast<double>(params->beta),
    static_cast<double>(input->params.scale), kScaledDiffIntegerBits,
    &op_data->input_multiplier, &input_left_shift);

由于使用的是 Double-rounding(文末附了Single-Rounding 和 Double-Rounding的区别)

const double max_real_multiplier = (1LL << 31) - 1.0;

1
2
3
const double input_beta_real_multiplier =
    std::min<double>(beta * input_scale * (1 << (31 - input_integer_bits)),
                    max_real_multiplier);

其中，

  • beta: 1.000000
    • Used even when beta defaults to 1.0.
    • 即使 beta 被设置为默认值 1.0，它不会被忽略，而是仍然参与计算。
  • input_scale: 0.091732
  • input_integer_bits: 5
    • static const int kScaledDiffIntegerBits = 5;
    • 这是设置的固定值
  • max_real_multiplier: 2147483647.000000
    • 使用的是 Double-rounding
    • const double max_real_multiplier = (1LL << 31) - 1.0;

得到 input_beta_real_multiplier: 6156025.000000

然后是函数 

1
2
QuantizeMultiplierGreaterThanOne(input_beta_real_multiplier,
                                 quantized_multiplier, left_shift);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
if (double_multiplier == 0.) {
  *quantized_multiplier = 0;
  *shift = 0;
  return;
}
const double q = std::frexp(double_multiplier, shift);
auto q_fixed = static_cast<int64_t>(TfLiteRound(q * (1LL << 31)));
  if (q_fixed == (1LL << 31)) {
  q_fixed /= 2;
  ++*shift;
}
if (*shift < -31) {
  *shift = 0;
  q_fixed = 0;
}
*quantized_multiplier = static_cast<int32_t>(q_fixed);

计算结果是

  • quantized_multiplier = 1575942400
  • left_shift = 23

然后是函数

1
2
3
op_data->diff_min =
    -1.0 * tflite::CalculateInputRadius(kScaledDiffIntegerBits,
                                        op_data->input_left_shift);
1
2
3
4
5
6
7
8
const double max_input_rescaled =
    1.0 * ((1 << input_integer_bits) - 1) *
    (1LL << (total_signed_bits - input_integer_bits)) /
    (1LL << input_left_shift);
// Tighten bound using floor.  Suppose that we could use the exact value.
// After scaling the difference, the result would be at the maximum.  Thus we
// must ensure that our value has lower magnitude.
return static_cast<int>(std::floor(max_input_rescaled));

通过 floor 操作对边界进行收紧，使计算结果不会超过允许的最大值或最小值。 假设可以使用精确的浮点数值进行计算。如果直接使用精确值进行放缩（scaling），计算结果可能正好达到边界值（如最大值 127）。但是实际计算中，任何额外的误差都可能导致结果超出边界。因此，为了避免超出范围，我们需要保证数值的绝对值低于或等于边界值。使用 floor 是一种方法，可以确保数值朝着更小的方向调整，从而满足边界要求。

通过向下取整，确保计算结果不会超出规定的范围，从而避免数值的溢出问题。

input_integer_bits = 5 input_left_shift = 23 total_signed_bits = 31

op_data->diff_min = -248 op_data->input_left_shift = 23 op_data->input_multiplier = 1575942400

在 TensorFlow 的量化运算中，double-rounding 和 single-rounding 是处理整数运算中舍入过程的两种策略。它们在计算中间结果和最终结果时的处理方式不同，对精度和性能有一定影响。

  1. Single-Rounding (单次舍入)

单次舍入是在完成量化运算后，直接对结果进行一次舍入操作。 • 过程： • 直接将运算的中间结果（通常是乘法后的积）除以一个缩放因子，并进行一次舍入操作。 • 用于快速实现，但在一些边界情况（比如舍入时丢失低位信息）下可能会有轻微的误差。

  1. Double-Rounding (双次舍入)

双次舍入是一个更精确的舍入策略，通过两次独立的舍入操作，减少了舍入误差。 • 过程： 1. 首先对乘法结果进行一次初步舍入，保留更多的有效位（通常在中间的高精度计算中使用）。 2. 再根据目标量化范围对初步舍入后的结果进行二次舍入。

  • Single-Rounding：
    • 通常在硬件限制较多（如嵌入式设备）的 TensorFlow Lite Micro 中实现。
    • 适合性能优先的场景。
  • Double-Rounding：
    • 用于更高精度要求的 TensorFlow Lite 和 TensorFlow 图层之间的累积计算。
    • 对浮点到定点转换中的精度保留尤为重要。
Thanks for your support.