Marlin Kernel是IST-DASLab 开发的GPTQ量化模型高性能 FP16(activation) x INT4(weight) GEMM算子实现,在现有W4A16 GEMM Kernel中,Marlin Kernel性能是最好的。
作为一个不会cuda的小白,研究完marlin算子之后神清气爽,
【长文预警 & 多图预警】
准备工作
分析工具
先把工具学习了,学习 nsight-compute。 NVIDIA Nsight
Compute 是一款适用于 CUDA
应用程序的交互式内核分析器。它通过用户界面和命令行工具提供详细的性能指标和
API 调试。
【CUDA进阶】深入理解 Nsight System 和 Nsight Compute
搭建环境
git clone https://github.com/IST-DASLab/marlin.gitexport TORCH_CUDA_ARCH_LIST="8.6"(这里要根据实际的版本来)pip install .python test.py
我是先读了论文,看了一些大佬的分析文章,比如 Marlin W4A16&W4A8代码走读、fp16*int4计算kernel--MARLIN代码走读 、 MARLIN: Mixed-Precision Auto-Regressive Parallel Inference on Large Language Models论文解读等,以及NVIDIA 官方指导文档, 然后开始进行代码的详细分析,慢慢学会了 cuda 和 marlin 。
开始分析
在 test.py 中起一个 m = 128, sms = 5 的
marlin.mul
即 self.run_problem(128, 768, 256, -1, -1)。
⚠️注意:本文全部使用这个case的数值进行带入。即
- m = 128
- k = 256
- n = 768
这个算子里面的变量不要老是按照拿到的数进行理解,要结合代码进行理解。
接下来进入 marlin_cuda_kernel.cu 文件的
marlin_cuda 函数逐步分析。
int marlin_cuda()函数
变量分析
1 | int tot_m = prob_m; |
由于传入的prob_m = 128,则
tot_m = 128,将其除以16并进行上取整,得tot_m_blocks = 8,这里是整除,没有进行pad,所以pad计算出来也就是0。
1 | if (sms == -1) |
这里由于指定了sms = 5,所以不会走后面的代码,否则会获取指定
CUDA 设备(dev)的多处理器数量。
1 | if (thread_k == -1 || thread_n == -1) { |
如注释所说:对于小批量处理来说,较好的分区(better partioning) 比 较好的计算资源利用(better compute utilization) 稍微更重要。在目前的例子中,prob_m = 128,所以得到的分区是
thread_k = 64thread_n = 256
1 | int thread_k_blocks = thread_k / 16; |
thread_k_blocks = 64/16 = 4thread_n_blocks = 256/16 = 16
为什么是除以16呢?因为Marlin Kernel使用的Tensor Core指令为
m16n8k16size的MMA指令,所以一次MMA指令执行的矩阵size为m16n8k16。而Marlin Kernel在设计的时候,以n方向的2次MMA计算的矩阵作为一个基本的sub_tile,即sub_tile的尺寸为m16n16k16。——源自Marlin W4A16&W4A8代码走读
主循环
接下来进入沿着m方向的循环
1 | for (int i = 0; i < tot_m_blocks; i += 4) { |
之前算过 tot_m_blocks=8,则
i = 0thread_m_blocks = 8prob_m = 128 - 16 * 0 = 128
由于 thread_m_blocks > 4,则
par = (16 * 8 - 0) / 64 = 2,这里可以看出来,m方向最大的基本执行单元是
64。
prob_m = 64 * par = 128, 这里是做了 pad 后的
prob_m。
然后i += 4 * (2 - 1),此时 i = 4。
我认为这里的(par - 1)的原因就是因为 for 循环里对 i 也有一个增加操作,
感觉二者结合起来看比较容易理解
(或者我认为改成i += 4 * par, for循环里不做i增操作更好理解一些)。此时,得到thread_m_blocks = 4。
i进入for循环的i+=4,不再满足循环条件,循环结束。
这里的par是2,如果par超过了max_par,那么应该就会多循环几次了。这一段的作用就是确定了m方向上的blocks = 4 和 parallel = 2。
目前的结果是
- thread_m_blocks = 4
- thread_n_blocks = 16
- thread_k_blocks = 4
- group_blocks = -1
于是进入CALL_IF(4,16,4,-1)
参数整理
各个参数都确定下来了,先画个图整理一下:
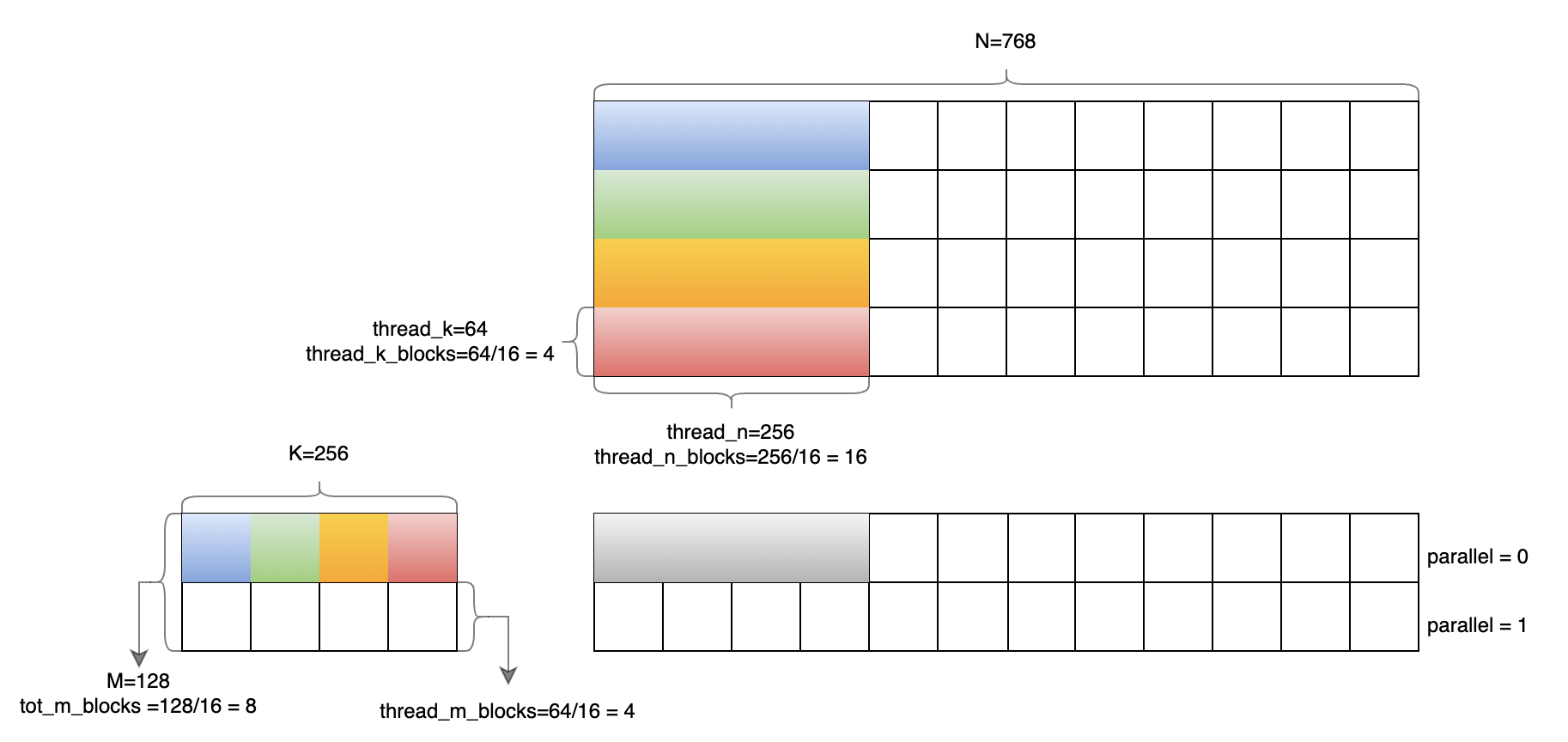
以M=128, K=256, N=768为例,每个小方格的大小是64x64,即 tile 的大小。
global void Marlin()函数
变量分析
开始核心代码 1
2
3
4
5int parallel = 1;
if (prob_m > 16 * thread_m_blocks) {
parallel = prob_m / (16 * thread_m_blocks);
prob_m = 16 * thread_m_blocks;
}
所以这几句的结果是
- thread_m_blocks = 4
- parallel = 2
- prob_m = 64
1 | int k_tiles = prob_k / 16 / thread_k_blocks; |
得到k_tiles = 4, n_tiles = 3, 所以目前一共有 k_tiles * n_tiles * parallel = 24个tile。而SM=5,因此,每个block需要计算的tile数量为5(24除以5后上取整,最后一个block只需要计算4个tile),即iters = 5.
条带分区
在讲接下来的部分前先讲一下marlin里面的stripe概念。
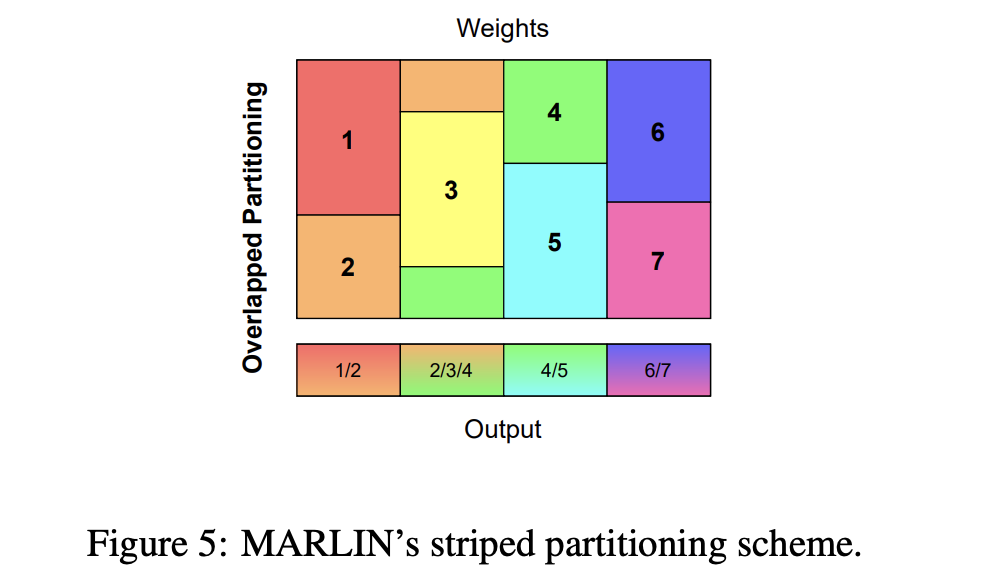
条带分区(Striped Partitioning)是一种在并行计算中常用的技术,特别是在大型矩阵乘法计算中,通过该技术可以提高负载均衡并最小化计算过程中的开销。
MARLIN内核中,条带分区是指由多个SM(流式多处理器)处理不同的矩阵“条带”,这意味着每个SM负责处理多块矩阵数据,这种分区方法保证了工作负载在处理器之间的均匀分布。
条带分区的核心思想是:
- 工作均衡分配:通过跨列或跨行分配条带,可以确保处理器均匀分配任务,防止部分处理器过载而其他处理器闲置。
- 减少全局同步开销:由于条带分区将任务均匀分配给各个处理器,减少了全局同步的需求,降低了并行计算中的通信开销。
- 提高缓存和内存效率:通过分割矩阵数据到条带,系统能够更有效地使用GPU缓存和内存带宽,从而最大化内存加载的吞吐量,并提高整体计算效率。
这种方法有助于在不同的GPU架构中优化计算性能,特别是在大规模深度学习模型的推理任务中。
本示例下的条带分区
前文讲过,每个block需要计算的tile数量为5。这里对B画个图表示一下:
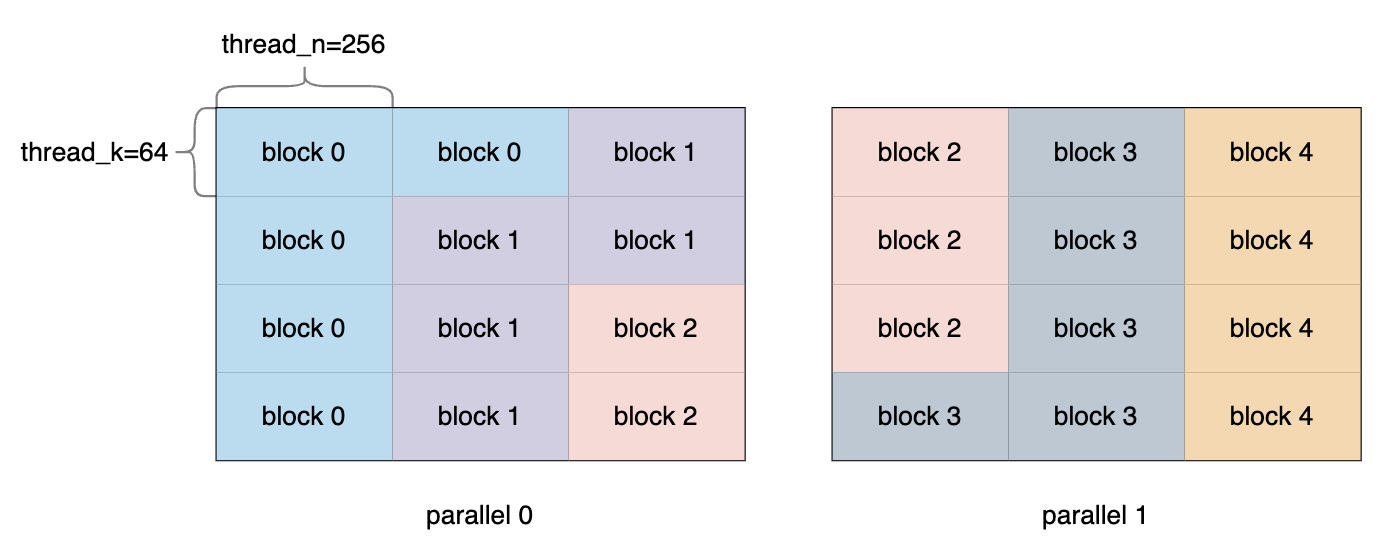
1 | int slice_row = (iters * blockIdx.x) % k_tiles; |
这两句有点抽象,结合上面的图,这里的计算其实是确定了每个block起始位置的纵坐标和横坐标。
| block 0 | block 1 | block 2 | block 3 | block 4 | |
|---|---|---|---|---|---|
| slice_row | 0 | 1 | 2 | 3 | 0 |
| slice_col_par | 0 | 1 | 2 | 3 | 5 |
指针推进
1 | // We can easily implement parallel problem execution by just remapping indices and advancing global pointers |
只需重新映射索引(remapping indices)和推进全局指针(advancing global pointers),就可以轻松实现并行问题执行。
比如这里的 n_tiles = 3,那对于 block 3 和 block 4
而言,要处理的就是第二个parallel,所以要推进一下A和C的指针。
init_slice()函数
接下来看比较容易迷惑的部分,如果不想细看这部分代码,可以直接看结论
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33// Compute all information about the current slice which is required for synchronization.
auto init_slice = [&] () {
slice_iters = iters * (blockIdx.x + 1) - (k_tiles * slice_col_par + slice_row);
if (slice_iters < 0 || slice_col_par >= n_tiles * parallel)
slice_iters = 0;
if (slice_iters == 0)
return;
if (slice_row + slice_iters > k_tiles)
slice_iters = k_tiles - slice_row;
slice_count = 1;
slice_idx = 0;
int col_first = iters * ceildiv(k_tiles * slice_col_par, iters);
if (col_first <= k_tiles * (slice_col_par + 1)) {
int col_off = col_first - k_tiles * slice_col_par;
slice_count = ceildiv(k_tiles - col_off, iters);
if (col_off > 0)
slice_count++;
int delta_first = iters * blockIdx.x - col_first;
if (delta_first < 0 || (col_off == 0 && delta_first == 0))
slice_idx = slice_count - 1;
else {
slice_idx = slice_count - 1 - delta_first / iters;
if (col_off > 0)
slice_idx--;
}
}
if (slice_col == n_tiles) {
A += 16 * thread_m_blocks * prob_k / 8;
C += 16 * thread_m_blocks * prob_n / 8;
locks += n_tiles;
slice_col = 0;
}
};
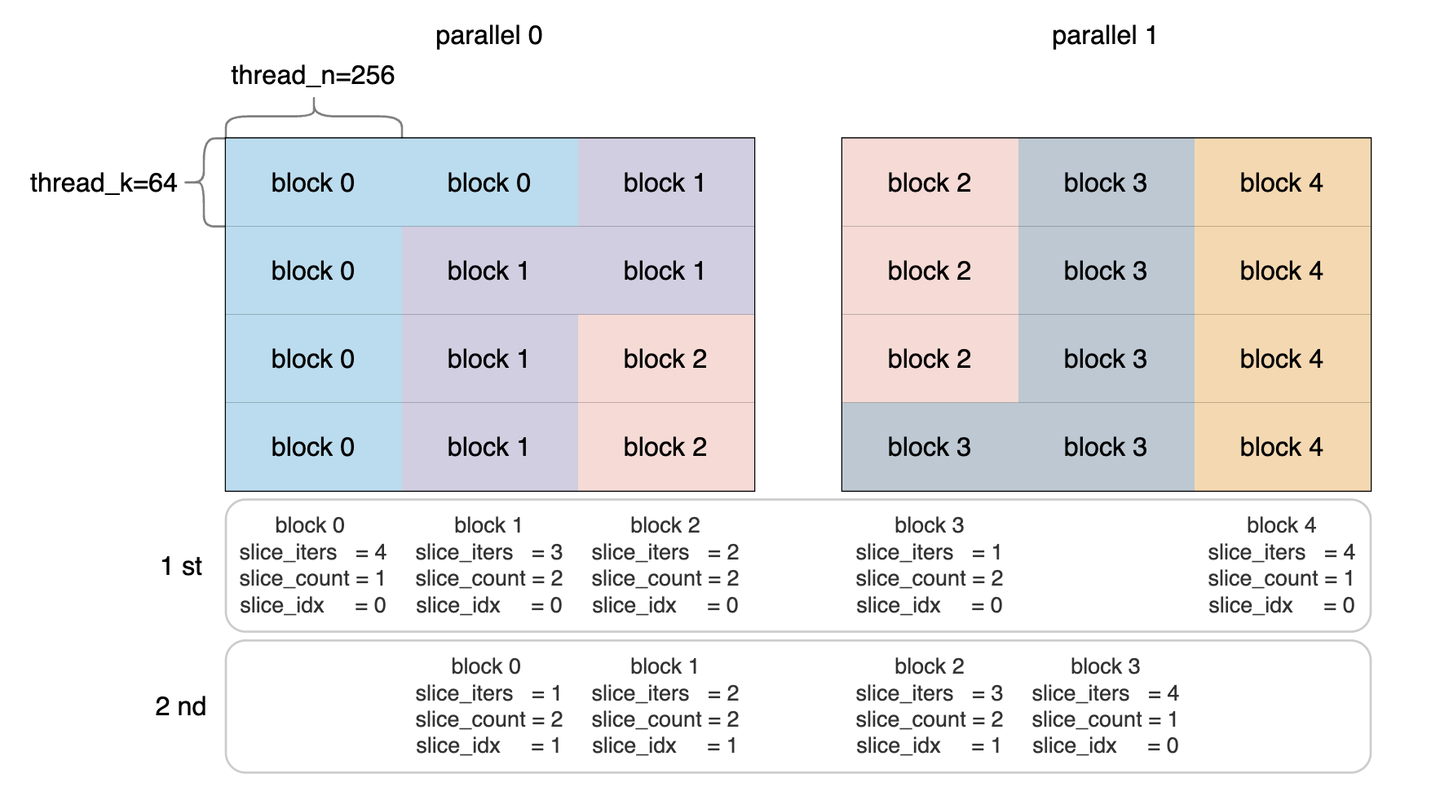
slice_iters
- 当前slice中的线程块(threadblock)块数
- block 0有4个,要迭代4次,block 1有3个,要迭代3次,依此类比
slice_count
- 当前slice中活跃线程块(active threadblock)的总数
- 第一个slice有1个(只有block 0),第二个slice有2个(有block 0和block 1)
slice_idx
- 当前slice中的线程块索引(index of threadblock)
- 这个索引从下到上编号。以第二个slice为例,block 1的idx是0,block 0的idx是1。
a_sh_wr_iters 变量
1 | int a_gl_stride = prob_k / 8; // stride of the A matrix in global memory |
接下来着重看一下 a_sh_wr_iters
这个变量:
从 Global mem 加载数据到 Shared mem 的时候,每一个 thread 会读取一个 int4(即4个int,128 bits),一个 thread blocks 256个线程需要分多次才能将完整的 tile 数据块读取完毕。
为什么用int4?
因为 kernel 使用的读取全局显存数据的`cp.async.cg.shared.global`指令最大处理长度是128 bits。在本文中,读取A矩阵tile需要的次数
a_sh_wr_iters = ceildiv(a_sh_stage, a_sh_wr_delta),
表示A的一个 tile 的 shared write 迭代次数。 其中,
- a_sh_stage = 512,表示A的一个 tile 的整体尺寸
- A矩阵一个 tile
为
[16 x thread_m_blocks, 16 x thread_k_blocks],所以大小是 64 * 64 / 8 - 除以8是因为A的指针是int4类型,4个int32_t, 128 bit,对应8个fp16,
- A矩阵一个 tile
为
- a_sh_wr_delta = 256,表示between shared memory writes。
- a_sh_wr_delta = a_sh_stride * (threads / a_gl_rd_delta_o);
- 8 * (256 / 8) = 256
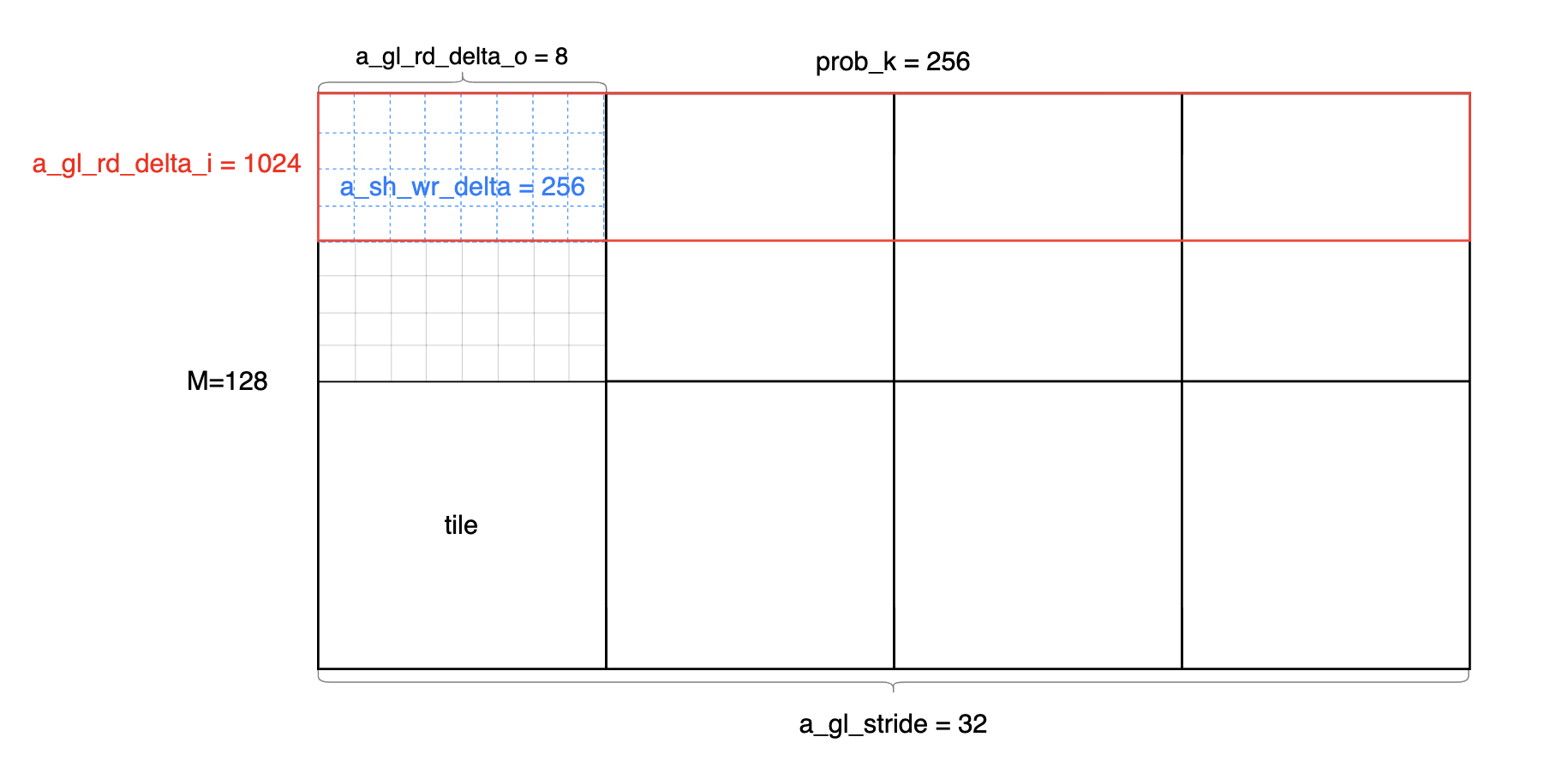
也就意味着,一个 thread blocks
256个线程能够读取256个int4,一个 tile 有 512
个int4,读取A矩阵 tile 要循环两次。在后面的
fetch_to_shared 函数里,一次是 fetch A 的一个
tile,这个地方会体现出循环了两次。
a_sh_wr_pred 变量
1 | // Precompute which thread should not read memory in which iterations; this is needed if there are more threads than |
在矩阵运算中预先计算出哪些线程在特定的迭代过程中不应该从内存中读取数据。这是为了优化计算资源的使用,特别是在以下两种情况下:
- 线程数超过所需的 tile 大小时:即当前的任务需要的线程数比实际提供的线程数要少,这可能会导致一些线程不需要参与内存读取。
- batchsize 不是 16 的倍数时:当批处理大小无法整齐地划分时,可能会出现某些线程无需读取数据的情况。
#pragma unroll:这个编译器指令提示编译器将循环展开(unroll),以减少循环控制的开销,优化性能。通常用于
GPU 编程中的小规模循环,因为展开循环可以减少分支跳转。
A矩阵的load
关于 bank conflict 的背景知识
Shared memory 是片上存储器,因此与 local memory 或 global memory 相比更高的带宽和更低的延迟。前提是线程之间没有 bank conflicts。
为了实现高带宽,共享内存被划分为大小相等的内存模块,称为 Banks,可以同时访问。因此,任何由 n 个地址组成的内存读取或写入请求都可以同时提供服务,从而产生比单个模块带宽高 n 倍的总带宽。
但是,如果warp内多个线程的内存请求的两个地址位于同一Bank中,则存在bank conflict,并且必须序列化访问。也就是说,Bank conflict 是在一个 warp 内,有2个或者以上的线程访问了同一个 bank 上不同地址的内存。
shared memory被分为 32 bank,每个bank的位宽是 4 byte。最大 transaction 大小为 128 bit。如果每个线程请求 16 bit,那么 warp 宽度将为每次请求(warp 宽度)的 512 bit。
当GPU每个线程访存大于 4 bytes,即每个 warp 大于
4 * 32 = 128 bytes 时,GPU 不会发出单个transaction,GPU
会将其分成 4 个 transactions(在这种情况下:T0-T7
组成一个transaction,T8-T15
是一个transaction,依此类推),每个transaction的宽度为 128 bit。
需要注意的是,bank conflicts 的确定是按 transaction 进行的,而不是按request、warp 或instruction进行的。
因此,每个 wrap 则会分割成多个 transaction 去执行,每个 transaction 保证线程内的访存不落在同一bank即可,所以当我们用最大访存指令时,需要保证1/4个连续线程不会存在地址重叠。
这也就是这个说法:
an access to Shared Memory will be conflict-free if the following conditions are satisfied across each warp:
- {T0, T1, .., T7} do not access the same 128-bit bank
- {T8, T9, .., T15} do not access the same 128-bit bank
- {T16, T17, .., T23} do not access the same 128-bit bank
- {T24, T25, .., T31} do not access the same 128-bit bank
A矩阵的解决方式
在marlin中,为了提高 load
效率,一般会使用向量化的读取命令,一次读取 128
bit,也就是 16 byte,对应4个bank。那么 8
个线程就可以一次完成 32 个bank 的load,所以问题简化为研究
T0 - T7 or T8 - T15 or T16 - T23
or T24 - T32 这 8 个线程内没有 bank 冲突。
如上文所讲,bank conflict 是针对单次 memory transaction 而言的。如果单次 memory transaction 需要访问的 128 bytes 中有多个 word 属于同一个 bank,就产生了 bank conflict。
对于A矩阵这种激活值矩阵而言,没有办法提前pack,因此 ldmatrix 指令读取的时候,会发生bank conflict。为了解决这个问题,需要对A矩阵的存储地址进行转换。对于ij位置可以通过转存到i(i ⊕ j)位置来避免冲突, 其中⊕是异或计算。
1 | auto transform_a = [&] (int i) { |
由于重映射计算较为复杂,且主循环进行了展开(unroll),所有的共享内存访问都是静态的,因此预先计算好重映射的读取和写入索引可以提高性能。
Swizzle 的实现
A矩阵的swizzle实现是transform_a这个函数,其实现很简单
row = i / a_gl_rd_delta_o算出来是在第几行i % a_gl_rd_delta_o算出来是在第几列(i % a_gl_rd_delta_o) ^ row进行异或,修改了列的位置a_gl_rd_delta_o * row + (i % a_gl_rd_delta_o) ^ row加上整体偏移
a_sh_wr_trans这个数组记录了进行swizzle的相关映射。
做了个动图看一下,就非常明晰了:
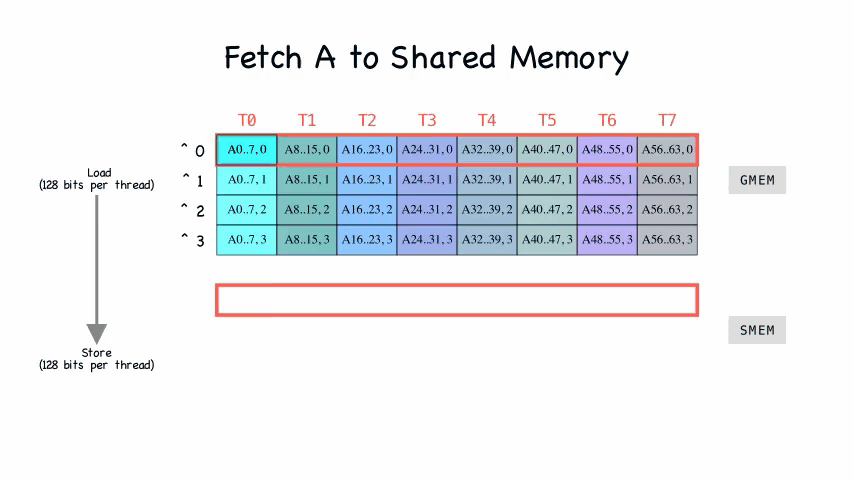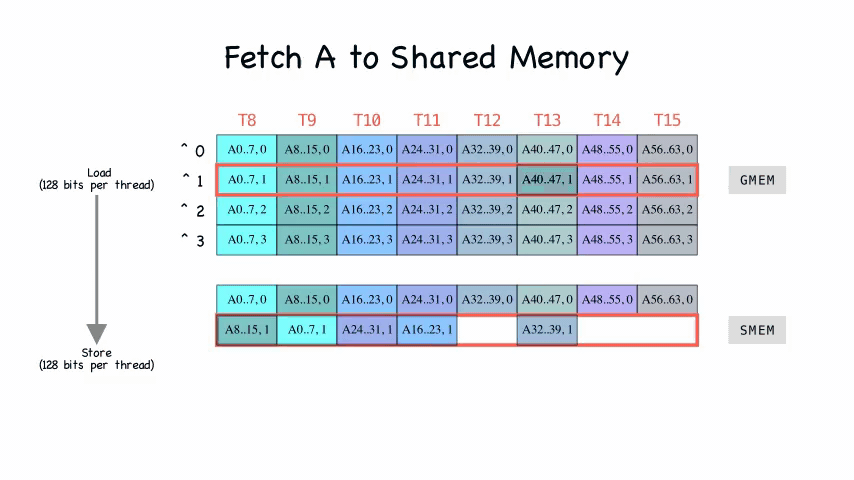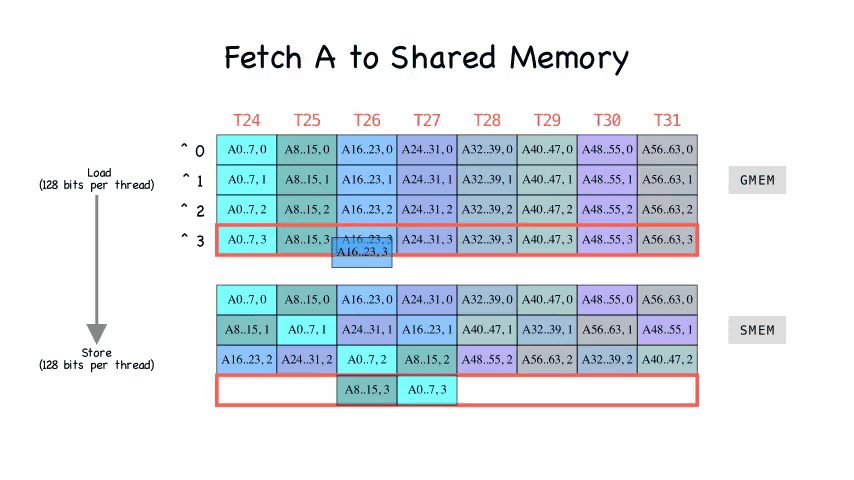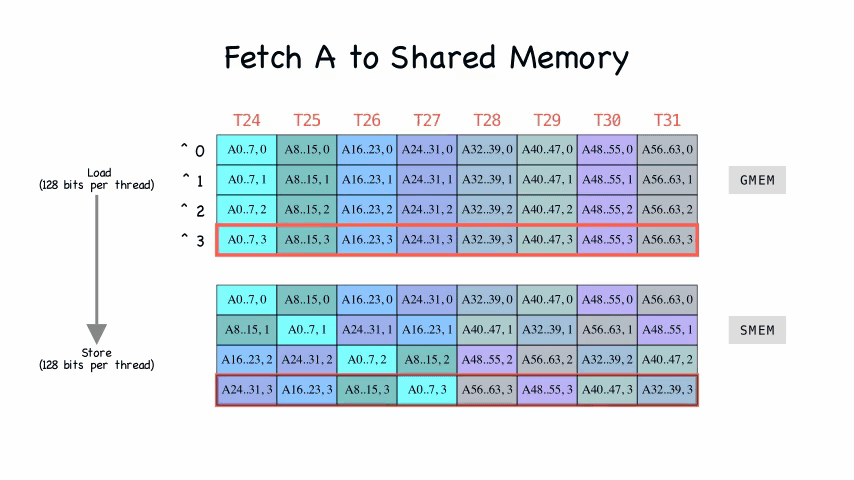
从 global memory 到 shared memory
搬运的代码实现是在fetch_to_shared函数中 1
2
3
4
5
6
7
8
9int4* sh_a_stage = sh_a + a_sh_stage * pipe;
for (int i = 0; i < a_sh_wr_iters; i++) {
cp_async4_pred(
&sh_a_stage[a_sh_wr_trans[i]],
&A[a_gl_rd_delta_i * i + a_gl_rd + a_gl_rd_delta_o * a_off],
a_sh_wr_pred[i]
);
}
其中 1
2
3
4
5
6
7
8
9
10
11
12
13// Predicated asynchronous global->shared copy; used for inputs A where we apply predication to handle batchsizes that
// are not multiples of 16.
__device__ inline void cp_async4_pred(void* smem_ptr, const void* glob_ptr, bool pred = true) {
const int BYTES = 16;
uint32_t smem = static_cast<uint32_t>(__cvta_generic_to_shared(smem_ptr));
asm volatile(
"{\n"
" .reg .pred p;\n"
" setp.ne.b32 p, %0, 0;\n"
" @p cp.async.cg.shared.global [%1], [%2], %3;\n"
"}\n" :: "r"((int) pred), "r"(smem), "l"(glob_ptr), "n"(BYTES)
);
}
cp.async 指令用于从全局内存异步拷贝数据到共享内存,不会阻塞其他计算操作。后面在讲流水线的时候还会再提到这块。
通过 pred 参数,允许控制是否执行这次异步拷贝。它用于处理批处理大小不是 16 的情况,确保在某些条件下可以跳过无效的数据拷贝操作。
16 字节是 GPU 进行全局到共享内存拷贝的一个高效的最小块,这样能够提升拷贝效率。
load到寄存器
接下来看一下A矩阵是怎么load到寄存器的。
1 |
|
可以看到,在 shared memory 到 frag 的过程中,用到了
a_sh_rd_trans
进行索引,而这也是通过上述的transform_a函数实现的,相当于往shared
memory写的时候是按照异或规则写的,读的时候也要按照异或规则读出来,这样才能正确地映射。
说一下题外话:
其实这里我纠结了很久,关于bank conflict 和
swizzle的内容我能够理解,但是我不能理解 marlin 用 swizzle
实现 bank conflict free: 在 marlin 中,A矩阵是 row-major
排布的,所以我一直疑惑为什么需要进行 swizzle :这个矩阵在 global memory
本身就是 row-major 排布的,岂不是按照原始顺序 load 到 shared
memory,然后顺序读取的话也不会 bank conflict?
为此我在cuda的swizzle是怎么实现bank conflict free的?进行了提问,Arthur的回答我认为很合理,即:
- swizzle 是在更复杂访问模式下,确保每个线程不会访问到相同的memory bank。
- 如果矩阵是row-major的且读取是连续的,那么可能无需swizzle操作就能避免bank conflict。
- 但如果存在交错访问或者更复杂的访问模式,则swizzle是有必要的,用以确保bank conflict free。
作为一个cuda小白最开始对这里非常疑惑,这里整理一下看过的一些相关资料:
- cute 之 Swizzle - reed
- cute Swizzle细谈 - 进击的Killua
- cute swizzle - shengying.wei
- CUDA编程概念:什么是bank conflict? - likewind1993
- [深入分析CUTLASS系列] 0x03 cutlass 源码分析(二) --- bank conflict free 的shared memory layout (附tvm等价pass) - JoeNomad
- 搞懂 CUDA Shared Memory 上的 bank conflicts 和向量化指令(LDS.128 / float4)的访存特点 - Alan 小分享
- How to understand the bank conflict of shared_mem
后来发现,如果不做 swizzle 其实是会发生 bank conflict
的,有一个细节:
在计算a_sh_rd_trans的时候 1
2
3
4
5
6
for (int i = 0; i < b_sh_wr_iters; i++) {
for (int j = 0; j < thread_m_blocks; j++)
a_sh_rd_trans[i][j] = transform_a(a_sh_rd_delta_o * i + a_sh_rd_delta_i * j + a_sh_rd);
}
要注意输入a_sh_rd变量:
1 | // Shared read index. |
这里估计是最难懂的一点,fp16*int4计算kernel--MARLIN代码走读 中解释了这一点:
第一行结合关于ldmatrix的说明,在 thread 0-32 分别获取对应 ldmatrix 需要的地址。这里可以看出确实是需要做swizzle操作。
第二行的 (thread_n_blocks / 4) 的逻辑:
256个线程,至少需要 b_sh_wr_iters 次后处理完一行,那就需要一次读取
thread_k_blocks/b_sh_wr_iters个 SUB_TILE。thread_k_blocks/b_sh_wr_iters = threads/8/thread_n_blocks为了能够利用资源,如果不重复读取,就会处理
threads/32个SUB_TILE。但是我们可以重复读取A矩阵来进行乘法后再归约,那么就有
threads/32/x = threads/8/thread_n_blocks因此
x = thread_n_blocks/4这就是
thread_n_blocks/4的由来。因此A矩阵,在LDMATRIX后,有重复矩阵。
如果仔细分析的话,可以这么理解:
- 实际上的GLOBAL IO没有变化,还是GLOBAL->SHARED的大小
- 运算并没有变多,B矩阵一直在变化,所以不会有重复计算。
简单来说就是为了配平IO和MMA操作,做的妖操作。fp16*int4计算kernel--MARLIN代码走读
这里画了一个图展示Global memory -> Shared Memory -> Frag 的过程:
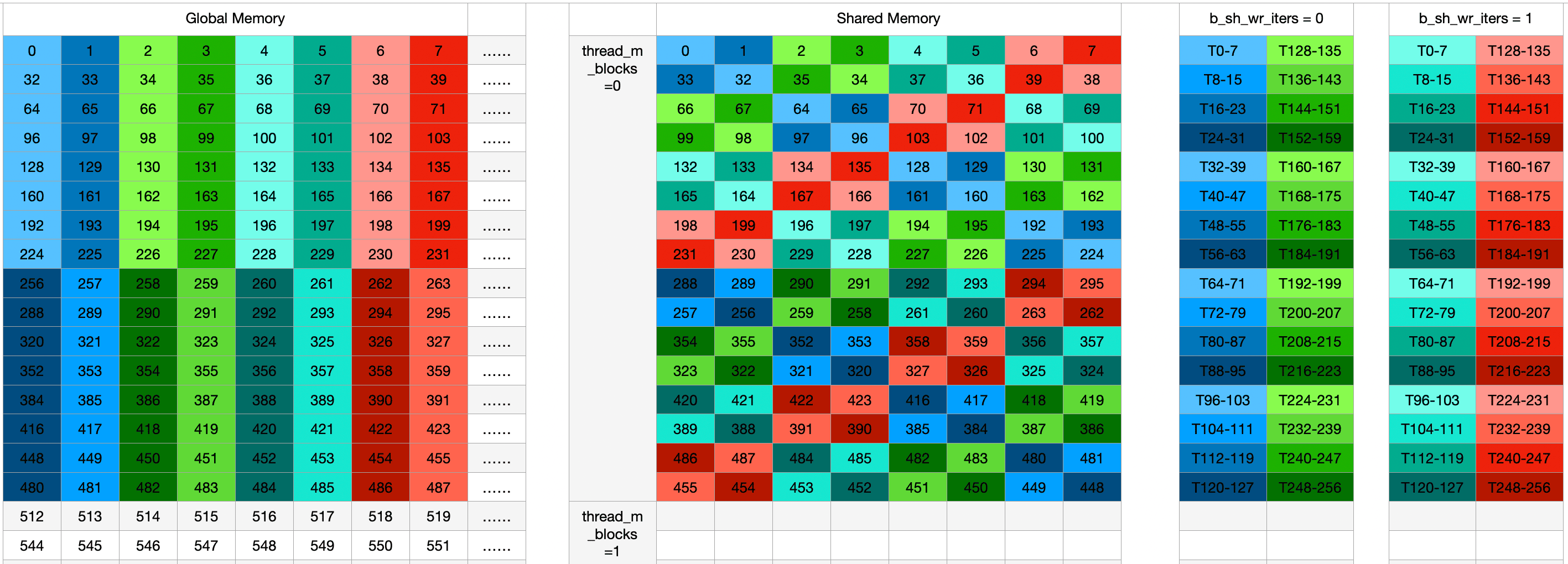
需要注意的是,ldmatrix 指令从 shared mem
加载数据到寄存器时会自动处理,使得寄存器中的数据满足这种特定的
layout。
ldmatrix函数
CUTLASS CuTe GEMM细节分析(一)——ldmatrix的选择 一文中指出了ldmatrix在加载地址上的灵活性,也就是ldmatrix并不要求这8个行在Shared Memory上连续存储,但每个行内部必须是连续存储的。这一点解疑了我关于A整体不连续是怎么ldmatrix的这个疑问。
1 | // Instruction for loading a full 16x16 matrix fragment of operand A from shared memory, directly in tensor core layout. |
Warp-level matrix load instruction: ldmatrix
这里使用了ldmatrix.sync.aligned.m8n8.x4,第二、三、四个矩阵的元素按照上表的布局加载到每个线程的后续目标寄存器中。
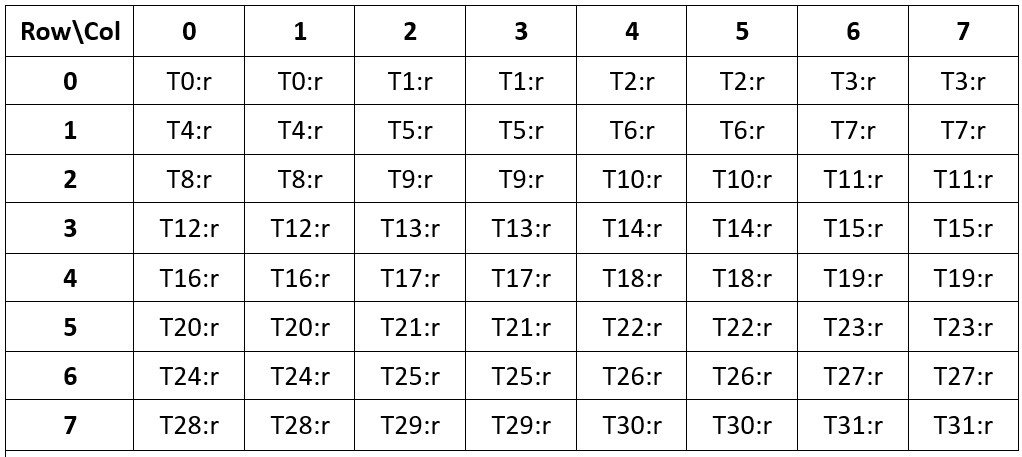
这样,A矩阵就被按照特定的 layout 加载到了寄存器中。而这个 layout 又是 mma 指令所需要的:
在 matrix-fragments-for-mma-m16n8k16-with-floating-point-type中可以看到 Multiplicand A 的 The layout of the fragments held by different threads:

B矩阵的load
B矩阵的load相对简单,没有做swizzle。因为是顺序 fetch 到 SMEM,再顺序 fetch 到 frag,B矩阵经过重排,使得MMA计算需要的[8, 16] tile全部处于一行,所以也不会有 bank conflict。
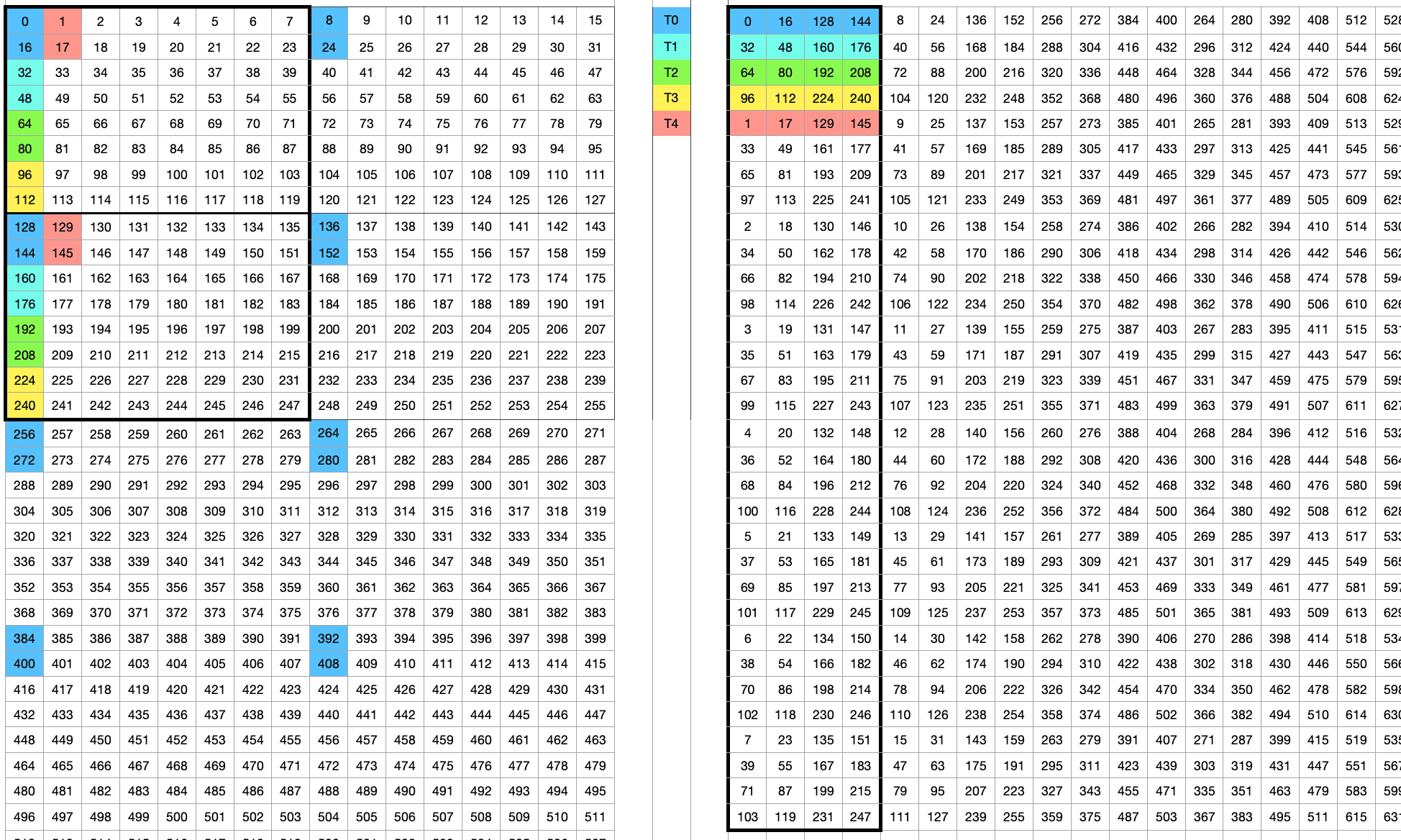
矩阵排布
需要关注的是在算子之前的矩阵的排布,也就是 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18perm = []
for i in range(32):
perm1 = []
col = i // 4
for block in [0, 1]:
for row in [
2 * (i % 4),
2 * (i % 4) + 1,
2 * (i % 4 + 4),
2 * (i % 4 + 4) + 1
]:
perm1.append(16 * row + col + 8 * block)
for j in range(4):
perm.extend([p + 256 * j for p in perm1])
perm = np.array(perm)
interleave = np.array([0, 2, 4, 6, 1, 3, 5, 7])
perm = perm.reshape((-1, 8))[:, interleave].ravel()
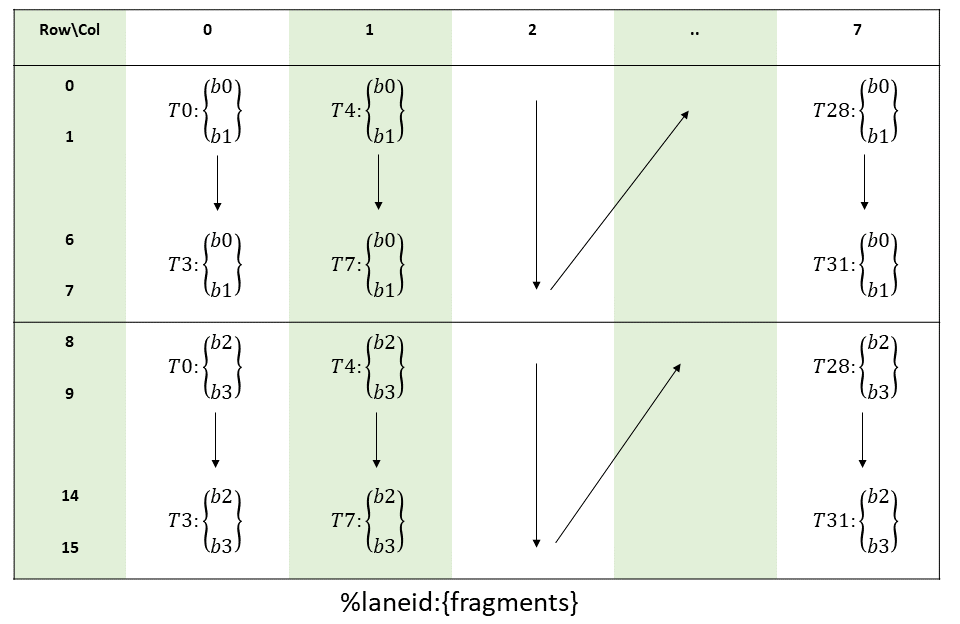
当然,后面还是做了一个 interleave 操作的,所以 B 的真正排布是在这个基础上做了 interleave 的,但是在进行dequant的时候又反interleave 了,所以这里的分析就不管interleave了,更直观一些。
matmul
1 | // Execute the actual tensor core matmul of a sub-tile. |
关于dequant这个函数,我之前在 WeightonlyGEMM:
dequantize_s4_to_fp16x2代码解析 详细分析过。思路是一样的,区别就是
marlin 想要 signed int4 输出,于是将 -8 这个
symmetric zero point 直接融合到 SUB 和 ADD 的
magic number 中。
1 | __device__ inline FragB dequant(int q) { |
这里仅以 e0 和 e1 为例:
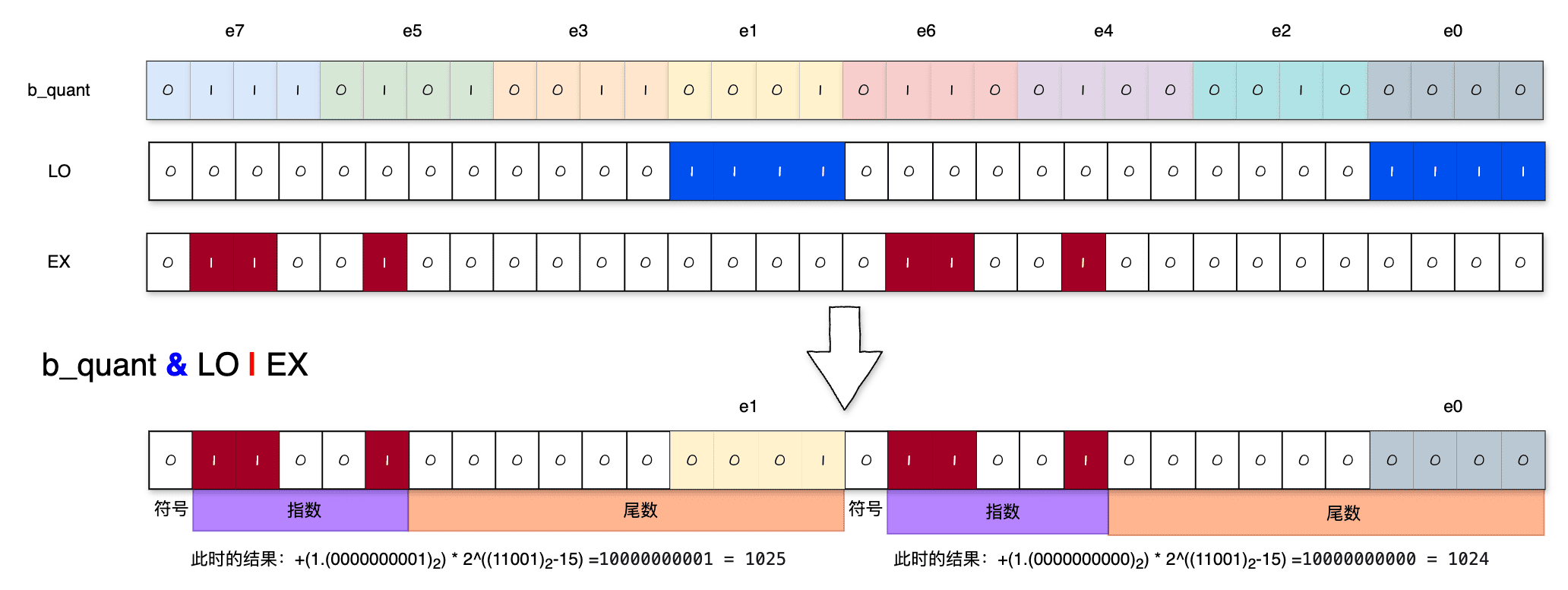
进行 lop3 操作后,提出来 e0 和 e1
元素,但此时的结果是加了 2^10 的,因此要减去 1024,以及减 8 这个zero
point,SUB = 0x64086408 中的 6408 对应的就是
1032。
frag_b_quant 类型是 Vec<int, 4>,这里的 j
循环是对这4个int的循环。
FragB 类型是 Vec<half2, 2>,也就是说
dequant 函数计算后得到的是2个 half2.
对应关系是这样的:

对B进行dequant后,就进行了 mma 操作。
1 | for (int i = 0; i < thread_m_blocks; i++) { |
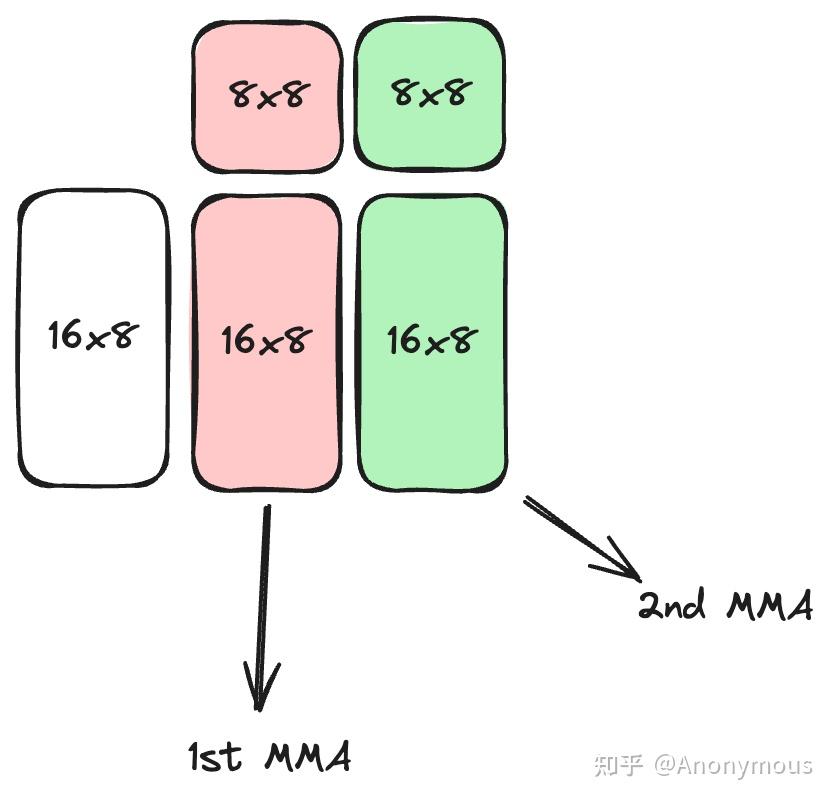
在m维度的循环是内循环,这样可以复用 b 的 dequant 结果。
一次matmul调用,外循环迭代4次,即在B矩阵的n方向计算4个16x16的B矩阵小块。内循环迭代thread_m_blocks次,即在A矩阵的m方向计算thread_m_blocks个16x16小块。每次内循环调用两次mma指令,完成一个 m16n16k16 的子块计算。
为什么每个matmul要计算4个B矩阵的 16x16 子块呢?这是因为从 shared mem 加载数据到 reg 的时候,每个线程读取 128 bit,每个 warp 个 32 线程总共读取 128x32 bits数据,而4个16x16 B矩阵块的数据量正好就是(16x16/8)x4x32 bits。这样可以使用所有的线程去加载计算所需要的数据。
mma 指令
其中 mma 是用的 mma.sync.aligned.m16n8k16.row.col.f32.f16.f16.f32
1 | // m16n8k16 tensor core mma instruction with fp16 inputs and fp32 output/accumulation. |
mma() 是张量核心的矩阵乘法函数,执行 A × B 的操作,并将结果累积到 frag_c 中。由于量化后的数据拆分为两部分(frag_b0 和 frag_b1),因此执行了两次乘法,每次使用不同的子块进行运算。
在mma的计算过程中SM就已经做了tile层面的b_sh_wr_iters 的归约操作。
A矩阵 和 B矩阵 的参数分析
在m = 128,k = 256,n = 768的情况下:
A 矩阵
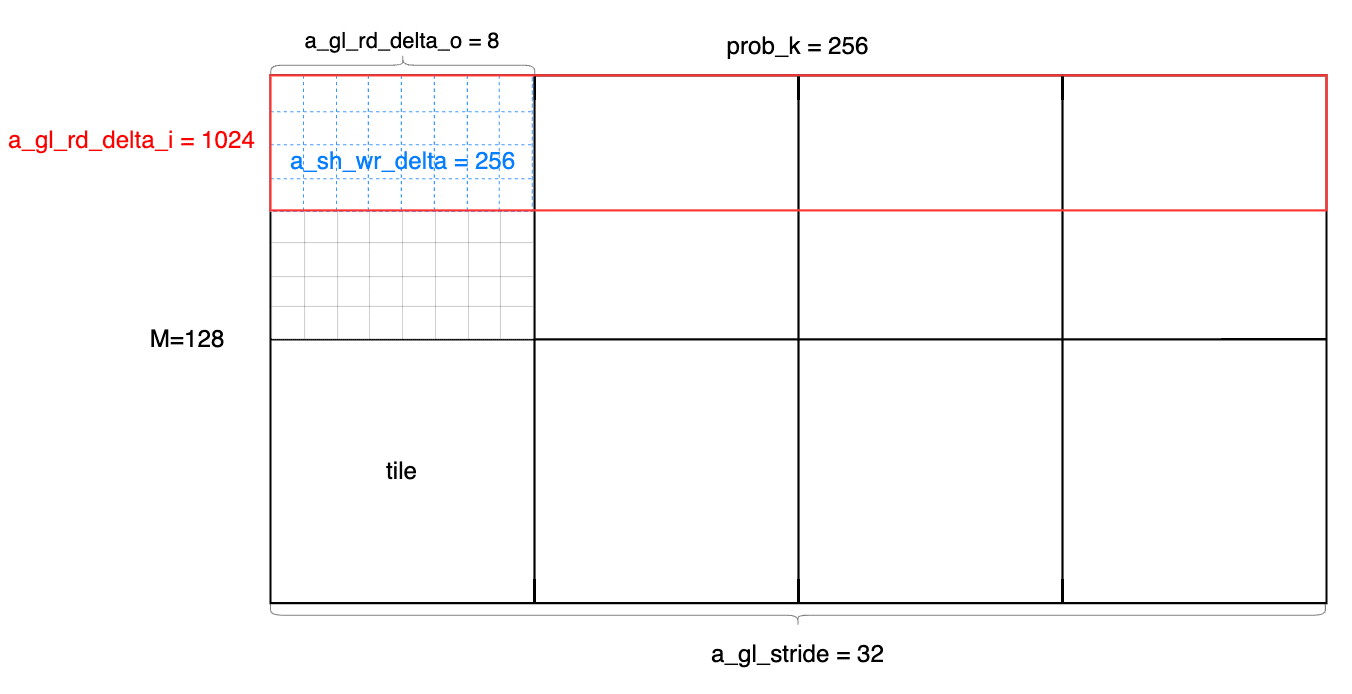
1
2
3a_gl_stride = prob_k / 8; // stride of the A matrix in global memory 每一个 thread 会读取一个 int4,所以除以 128/16=8
a_gl_rd_delta_o = 16 * thread_k_blocks / 8; // delta between subsequent A tiles in global memory
a_gl_rd_delta_i = a_gl_stride * (threads / a_gl_rd_delta_o); // between subsequent accesses within a tile
1
2
3
4
5
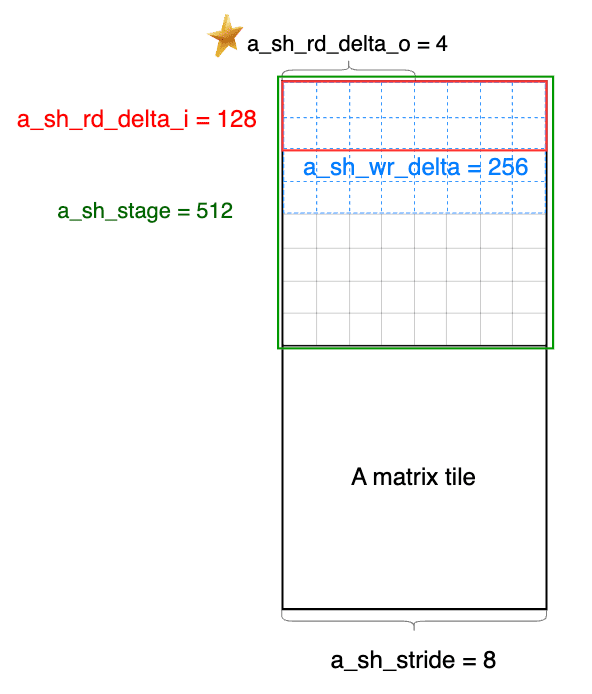
6a_sh_stride = 16 * thread_k_blocks / 8; // stride of an A matrix tile in shared memory
a_sh_wr_delta = a_sh_stride * (threads / a_gl_rd_delta_o); // between shared memory writes
a_sh_rd_delta_o = 2 * ((threads / 32) / (thread_n_blocks / 4)); // between shared memory tile reads
a_sh_rd_delta_i = a_sh_stride * 16; // within a shared memory tile
a_sh_stage = a_sh_stride * (16 * thread_m_blocks); // overall size of a tile
a_sh_wr_iters = ceildiv(a_sh_stage, a_sh_wr_delta); // number of shared write iterations for a tile
B 矩阵
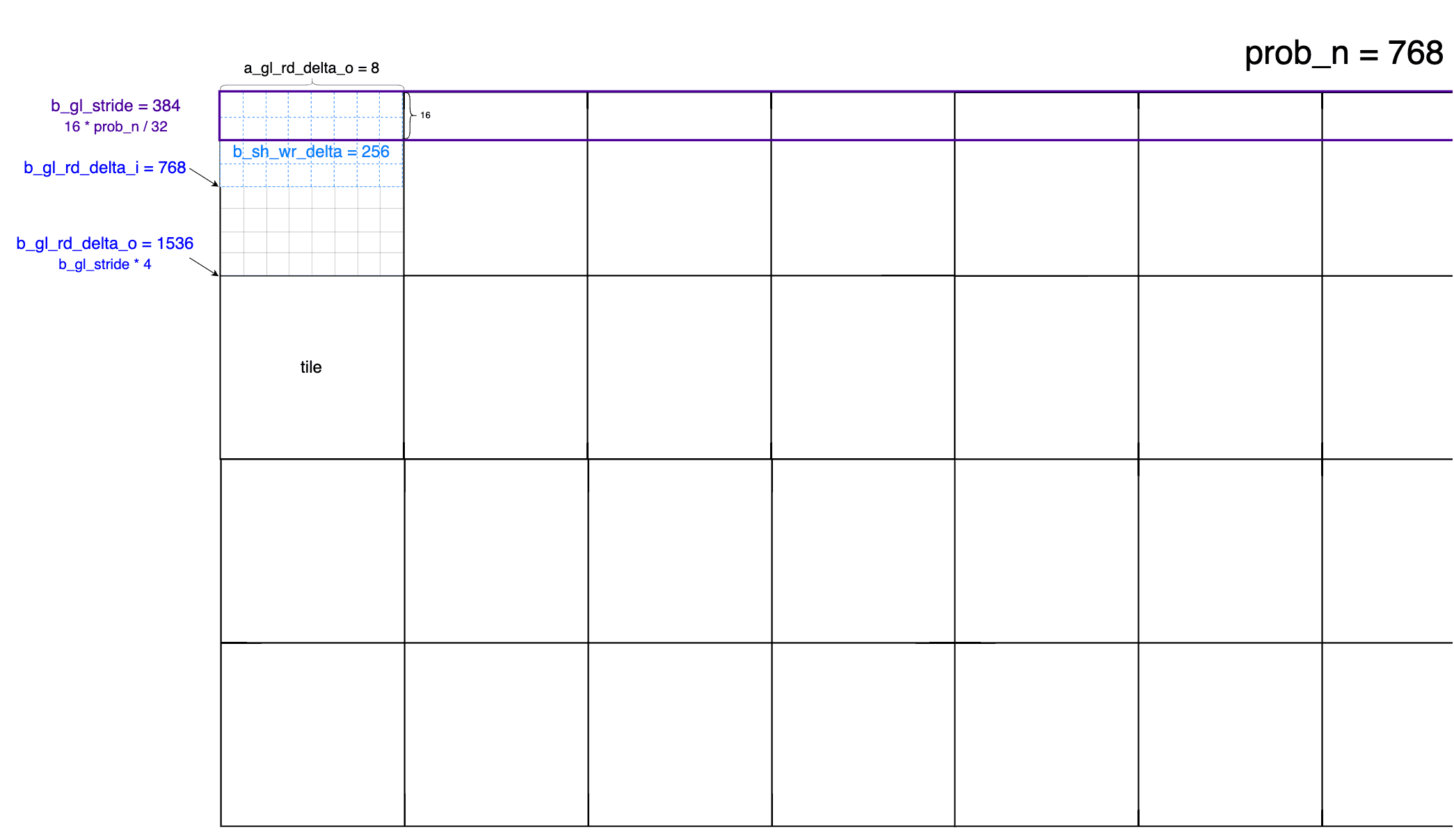
1 | b_gl_stride = 16 * prob_n / 32; |
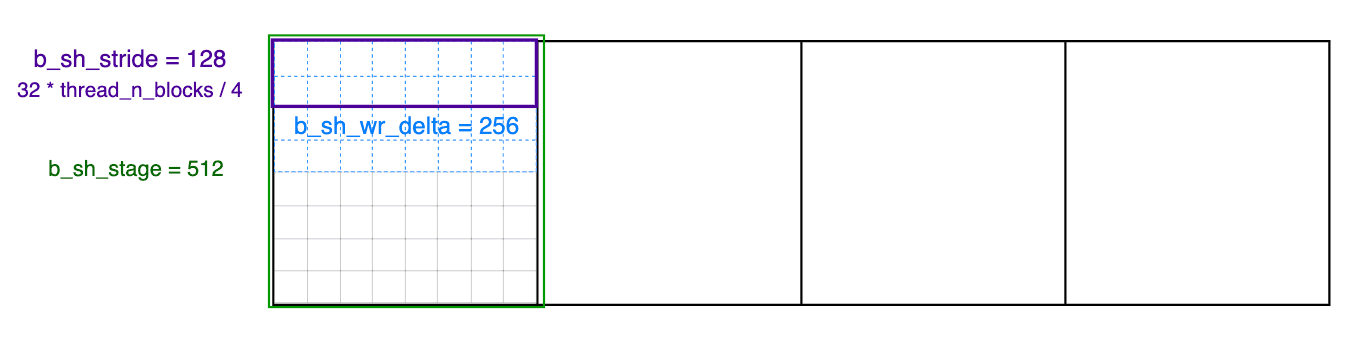
1 | b_sh_stride = 32 * thread_n_blocks / 4; |
b_sh_stride = 32 * thread_n_blocks / 4;
这里困扰了我很久,在这里一定要记录一下:
- 32 = 16 * 16 * 4 / 32
- 16 * 16 是warp大小
- 4是重复4次
- 32是类型转换 int4->INT4(128bit/4bit=32)
- 4是重复4次
Reduce


按照Marlin Kernel的Tile切分方式,一个C矩阵的Tile可能由多个thread
block参与计算。如上文,C矩阵第一个Tile只有 thread block 0
参与计算,而第二个Tile由 block 0 和 block 1
共同计算,两个 block 分别持有部分结果。
对于第一个 Tile 这种只由一个 block 参与计算的情况,由于一个 thread
block 中不同的 warp 分别持有部分结果,因此,只需要进行 thread block 内的
reduce,把不同 warp 持有的部分结果规约。这部分工作由
thread_block_reduce() 负责。thread_block_reduce() 利用
shared mem交换数据。
而对于第二个 Tile 这种由多个 block 参与计算的情况,则需要在进行
thread block 内的 Reduce 之后,再进行 block 间的 reduce,将多个 block
持有的部分结果进行规约。这部分工作由 global_reduce()
负责。global_reduce()利用 global mem 交换数据。
block reduce
frag_c 寄存器
先看一下 FragC frag_c[thread_m_blocks][4][2];
using FragC = Vec<float, 4>;mma后,一个线程是4个fp32;thread_m_blocks: 比较好理解,一个 tile 里面在 m 方向计算过 thread_m_blocks 个 16x16 小块;- 4: 在n方向计算4个16x16的B矩阵小块;
- 2: subtile 即
A(16,16) * B(16,16)分为2次 mma 执行。
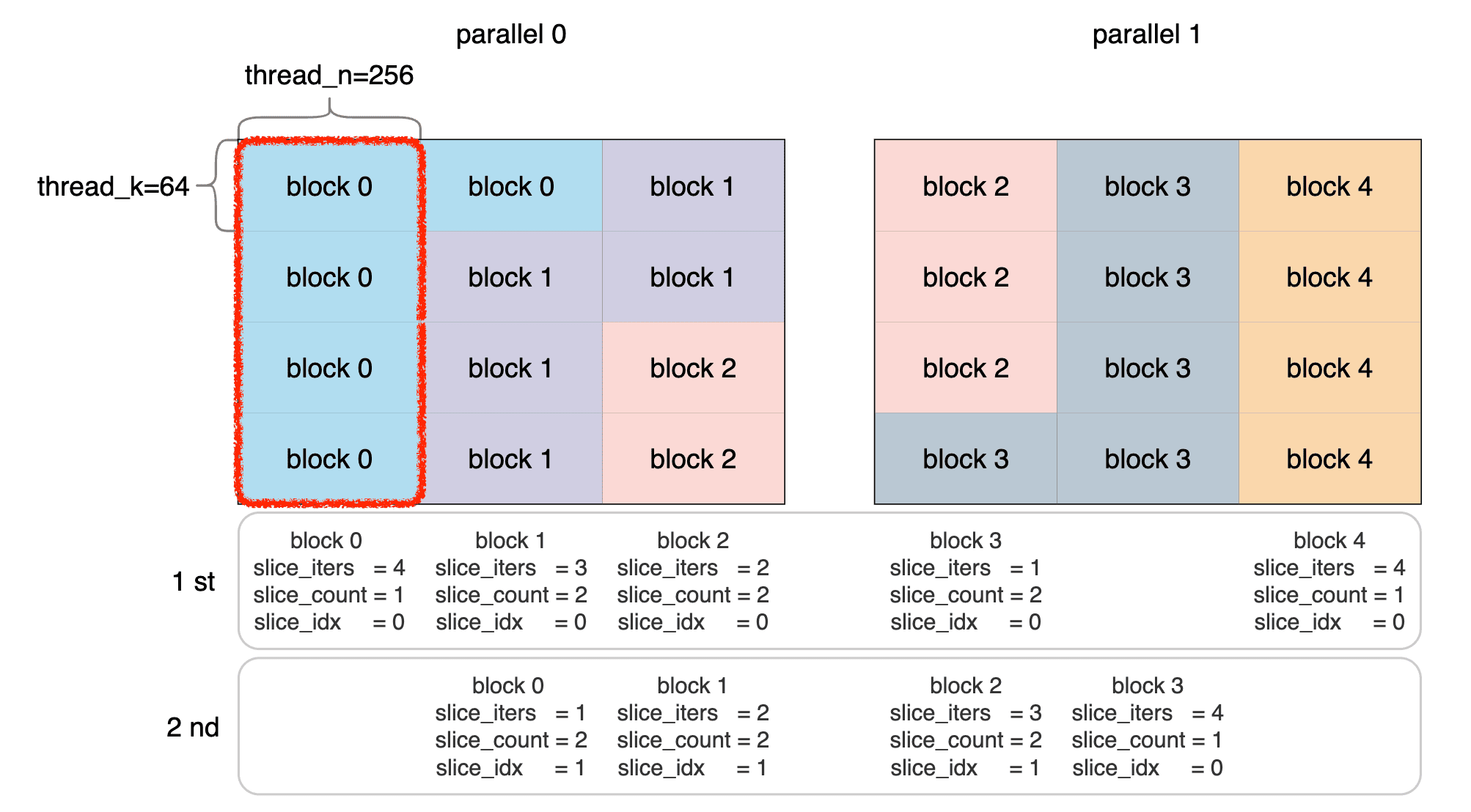
从 frag_c 的角度看第一个 slice 的过程:
zero_accums函数将frag_c清零- 循环
slice_iters次,frag_c的各个[thread_m_blocks][4][2]不断在做累加,实现了在 tile 层面的 b_sh_wr_iters 的归约。 - 当 slice_iters == 0
的时候,也就意味着做完这个block在这个slice里做完mma了,于是要进行
thread_block_reduce,在K维度做thread_k_blocks/b_sh_wr_iters的归约。
block reduce 分析
在许多并行计算的情况下,k 维度(内积的长度)可能非常大,因此通过将 k 维度切分为多个块可以增加并行计算的粒度和线程的利用率。
- k 维度的切分:为了增加并行计算的线程块(warps)的数量,这里选择将 k 维度进行切分。切分后的每个 k 维度的子块可以由不同的 warp 进行并行计算。
- 增加 warp 数量:通过将 k 维度切分,不仅可以增加参与计算的 warp 数量,还能更好地利用 GPU 的并行计算能力,提高整体吞吐量。
为了确保性能,代码选择只切分 k 维度,而保持 n 维度(列数)大小合理。这样可以保证每个线程块(warp)有足够的计算工作,但不会因为过多线程竞争导致 n 维度变得过大,从而降低局部数据重用的效率。
由于不同的 warp 都在并行处理相同的输出位置,因此每个 warp 只计算了部分的结果(partial sums),这些部分结果需要在最后进行归约(reduction)操作.通过在共享内存中累积每个 warp 的部分和,可以高效地进行归约操作,而不必依赖全局内存。这避免了全局内存带来的延迟,同时利用共享内存实现快速的同步和数据共享。
通过切分 k 维度,这段代码增加了并行度,从而提高了 GPU 的利用率。每个 warp 计算部分和的结果,最终需要通过共享内存进行归约操作,将多个部分和合并为最终结果。这种方式可以有效提升矩阵乘法的性能,同时利用共享内存的高效性来完成必要的同步操作。
代码
1 |
|
这段代码实现的是 并行的对数级共享内存归约(reduction)操作,通过减少内存读写操作来提高归约的性能。对数级归约是指通过每次减少一半的数据规模来加速归约操作,时间复杂度为 O(log(n)),这里通过逐步合并部分结果实现归约。
在并行计算中,不仅需要在每个 warp 内部进行局部归约,还需要在计算的最后阶段对多个 warp 产生的中间结果进行合并,得到最终的结果。
数据流向
由于每个线程的寄存器是私有的,其他线程无法访问,因此线程之间若需要共享数据或进行同步处理,必须通过共享内存来进行通信和数据交换。
所以block reduce只需要进行 REG->SHARED->REG
的转化,不涉及全局内存读取。而且这一过程避免了任何不必要的读取或写入迭代,例如,对于两个
warp,我们仅通过 warp 1 写入一次,仅通过 warp 0 读取一次。
global reduce
通过条状分区,同一列的数据会尽量集中在较少的线程块上处理,从而减少归约操作的频率。尽可能减少全局归约是优化并行程序性能的重要手段之一。
最终的归约操作是在 L2 缓存 中串行完成的。L2 缓存速度比全局内存快,但比共享内存慢。使用 L2 缓存进行归约操作具有以下优点:
- L2 缓存的优势:相比全局内存,L2 缓存的延迟较低,访问速度更快。在全局归约过程中,使用 L2 缓存可以加快数据的合并速度,减少内存带宽的消耗。
- 串行归约:归约操作是串行进行的,这可能是因为最终的输出数据较小,串行执行归约的开销很低。并且,串行操作可以简化编程复杂度,不需要额外的并行归约算法。
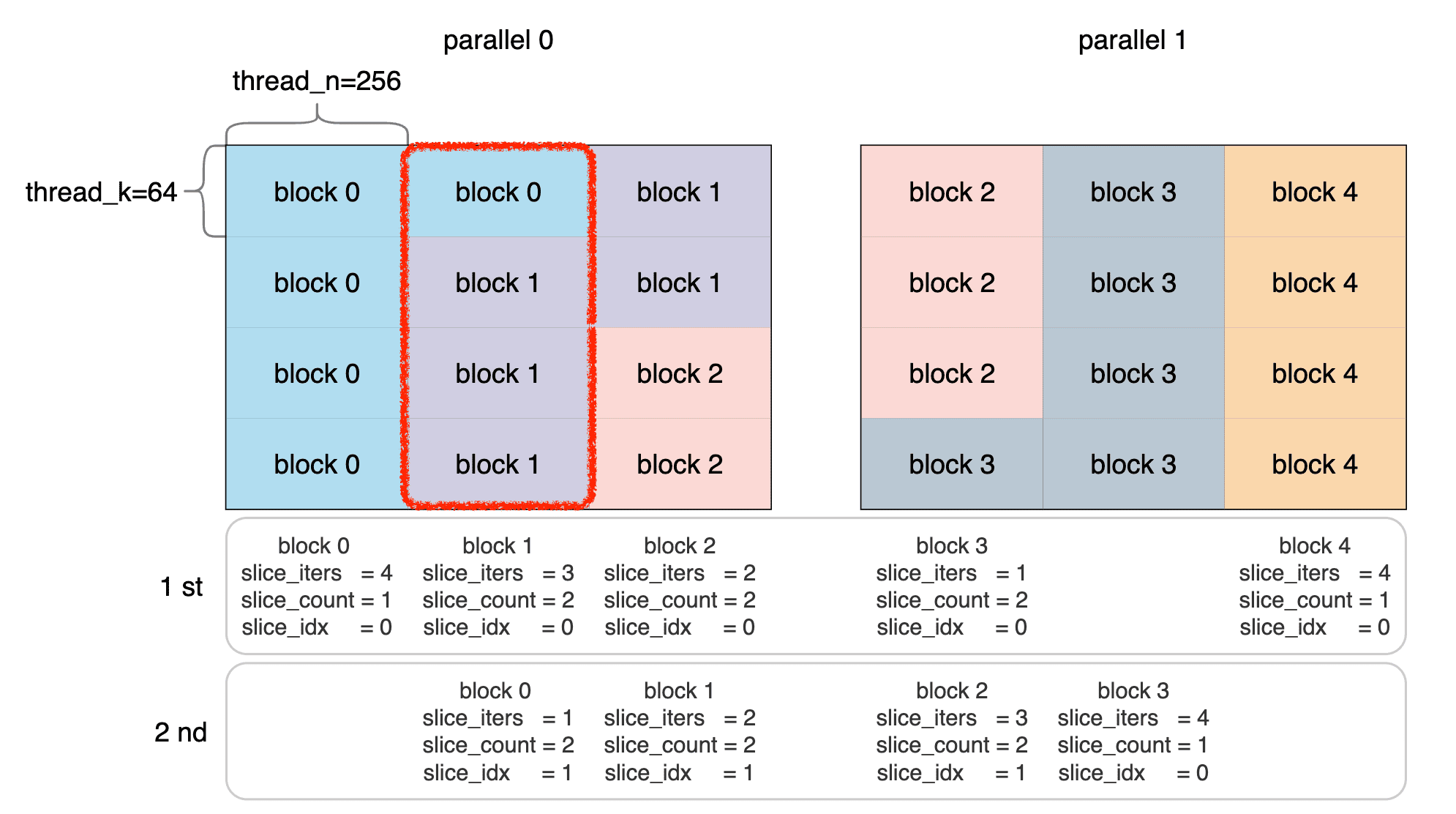
看一下第二个 slice 的过程:
- 第一次
start_pipes后,block1 进行了 3 次迭代(slice_iters),在最后一次做完mma后进行了thread_block_reduce - 第二次
start_pipes后,block0 进行了 1 次迭代(slice_iters),在做完mma后进行了thread_block_reduce - 注意此时
last = slice_idx == slice_count - 1为true(要注意slice_idx是numbered bottom to top)
这个slice的slice_count是大于1的,所以会进行global_reduce
1
2
3
4
5if (slice_count > 1) { // only globally reduce if there is more than one block in a slice
barrier_acquire(&locks[slice_col], slice_idx);
global_reduce(slice_idx == 0, last);
barrier_release(&locks[slice_col], last);
}
global_reduce的工作原理其实是按照 slice_idx
的顺序依次进行规约:
1)第一个slice(slice_idx==0),将自己持有的部分结果写到全局显存。
2)后续非最后一个slice从全局显存读取已经规约的结果,与自己持有的结果相加,结果写回全局显存。
3)最后一个slice从全局显存读取已经规约的结果与自己持有的结果相加。
global_reduce 函数
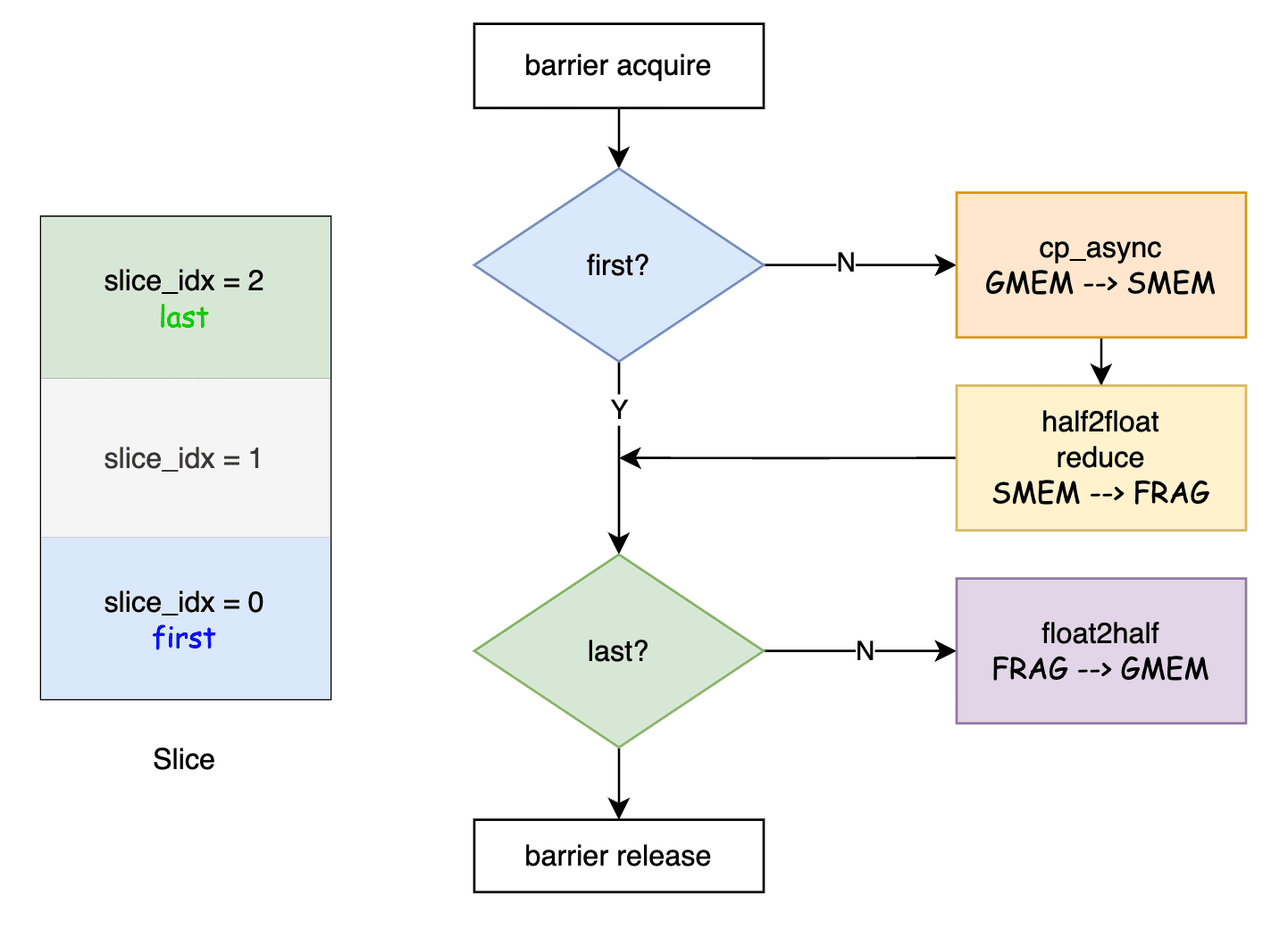
对照这个流程图,对于 slice_idx = 0 的 block
而言,是first,不是last,所以是将结果转成 half 类型后写到 global memory
里面;
对于 slice_idx = 1 的 block
而言,不是first,不是last,所以是先将 global memory 的结果fetch到 shared
memory,转成 float 后进行 reduce,结果转成 half 类型后写到 global
memory里面;
对于 slice_idx = 2 的 block
而言,不是first,是last,所以是先将 global memory 的结果fetch到 shared
memory,转成 float 后进行 reduce,结果还在寄存器里面
按照我的理解,slice_idx = 0 的 block 和
slice_idx = 1 的 block 是在一个 pipe里面,那么怎么保证
slice_idx = 1 的 block 在slice_idx = 0 的
block
存完之后再操作呢?这种按slice顺序进行reduce的行为由barrier_acquire
和 barrier_release 函数来保证的。
barrier_acquire 函数
1 | // Wait until barrier reaches `count`, then lock for current threadblock. |
只有线程块中的第一个线程(threadIdx.x == 0)会执行对 lock 的检查。这是为了避免同一线程块中的所有线程都同时访问全局内存,造成资源竞争。
asm volatile ("ld.global.acquire.gpu.b32 %0, [%1];\n" : "=r"(state) : "l"(lock));
这条内联汇编指令从全局内存中读取锁的值 lock,并将其存入 state。它使用了
CUDA 的 acquire
语义,这保证了在该点之前的所有读写操作对其他线程是可见的。
如果当前锁的值与 count 不一致,线程块中的第一个线程会一直循环,直到锁值等于 count。这意味着线程块会等待,直到其他线程块执行了对应的操作,修改了 lock 的值。
后面有一个线程同步,确保整个线程块中的所有线程在 lock 达到指定值之前不会继续执行后续代码。
这个函数整体是用于等待锁达到指定值,让线程块中的所有线程在达到barrier前等待。这是一个同步点,确保后续操作不会与前面已经发生的操作重叠。
barrier_release 函数
1 | // Release barrier and increment visitation count. |
在释放barrier前,先进行线程同步,确保线程块内的所有线程都已经完成了各自的工作,达到了barrier点。
仍然是线程块内的第一个线程执行锁的更新操作,避免多线程对同一锁进行竞争访问。
如果 reset 为 true,则将 lock 重置为 0
并立即返回,不再执行后续的释放操作。这用于在这个slice的最后一次global
reduce
asm volatile ("fence.acq_rel.gpu;\n");:这条指令是一个“获取-释放(acquire-release)”内存屏障,它确保在屏障释放前,当前线程块对共享数据的所有写操作对其他线程块是可见的。
asm volatile ("red.relaxed.gpu.global.add.s32 [%0], %1;\n" : : "l"(lock), "r"(val));:这里使用了
add.s32(32位整数加法)操作,通过原子操作将 lock 值加
1,表示当前线程块已经达到了屏障。其他等待这个锁的线程块就可以继续运行了。
这种加法操作使用了
red.relaxed.gpu.global.add,它是一个relaxed操作,不需要严格的同步模型,因此有助于性能优化。
这个函数整体是用于释放锁,并将锁的值加 1,表示当前线程块已经完成了当前阶段的工作。如果是在这个slice的最后一次global reduce,则重置锁,以便重新初始化同步机制。
这两个函数共同实现了线程块之间的同步机制,确保数据在不同线程块之间传递时的一致性,同时最大化性能优化。
workspace:是用来做global_reduce的标志位,shape为[n / 128 * max_par],由于n维度最小切分粒度为128,因此C矩阵最多被切分为n / 128 * max_par个slice,每个slice需要一个标志位。
write_result
global_reduce规约完不同thread block的结果之后,C矩阵Tile的结果规约在最后一个slice的寄存器中了,因此,最后一个slice负责把结果写回全局显存,这部分工作由write_result()负责。
write_result()先将结果写回shared mem,再从shared mem写回全局显存。同时,如果使用per_channel量化,则在这里会进行结果的scale操作。
因为共享内存访问比全局内存要快得多,所以先在共享内存中对结果进行重新排序,
1 | auto write = [&] (int idx, float c0, float c1, FragS& s) { |
res = __halves2half2(__float2half(c0), __float2half(c1))
将两个单精度浮点数压缩成一个半精度浮点数对
如果
group_blocks == -1,说明需要进行按列量化(per-column
quantization)。
最后,重排后的 half2 结果被写入共享内存 sh 的指定位置 idx。
1 | for (int i = 0; i < ceildiv(16 * thread_m_blocks, threads / (2 * thread_n_blocks)); i++) { |
共享内存中的数据被整理后,通过循环依次写入全局内存。线程逐步读取共享内存中的数据(sh),并写入全局内存的对应位置(C)。
任务调度
https://zhuanlan.zhihu.com/p/716412368
相比于CNN的卷积,LLM的矩阵乘有这样的特性:IO比乘法运算更重要,因此需要更加精致的优化。TILE的核心是在IO读取和计算之间的一种平衡,这种调度目前IO处理非常有优势。
疑惑的点:
矩阵A为什么是竖的 block reduce具体是哪些在reduce
参考资料:
https://arxiv.org/pdf/2408.11743
进击的Killua:MARLIN: Mixed-Precision Auto-Regressive Parallel Inference on Large Language Models论文解读
suluner:Marlin W4A16&W4A8代码走读
cutlass/media/docs/implicit_gemm_convolution.md at main · NVIDIA/cutlass
reed:cute 之 GEMM流水线
Optimizing Parallel Reduction in CUDA
ncu-rep
输入 m = 128, k = 256, n = 768
- 0_base.ncu-rep: 原始版本,不限制SM数量
- 1_base_sm5.ncu-sep: 限制SM数量为5
ncu --set full --target-processes all --kernel-name 'Marlin' --export base.ncu-rep python test.py
最开始设置 SM 为5,分析报告指出:
The grid for this launch is configured to execute only 5 blocks, which is less than the GPU's 82 multiprocessors. This can underutilize some multiprocessors. If you do not intend to execute this kernel concurrently with other workloads, consider reducing the block size to have at least one block per multiprocessor or increase the size of the grid to fully utilize the available hardware resources. See the Hardware Model description for more details on launch configurations.
于是解除对SM的限制,最终得到的报告如下:
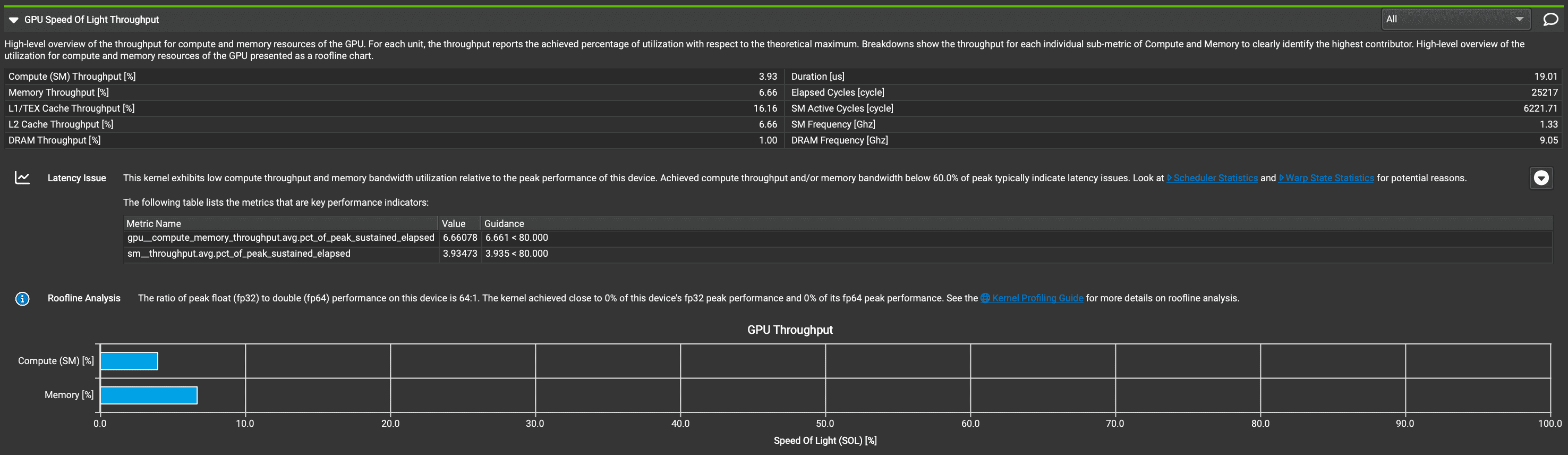

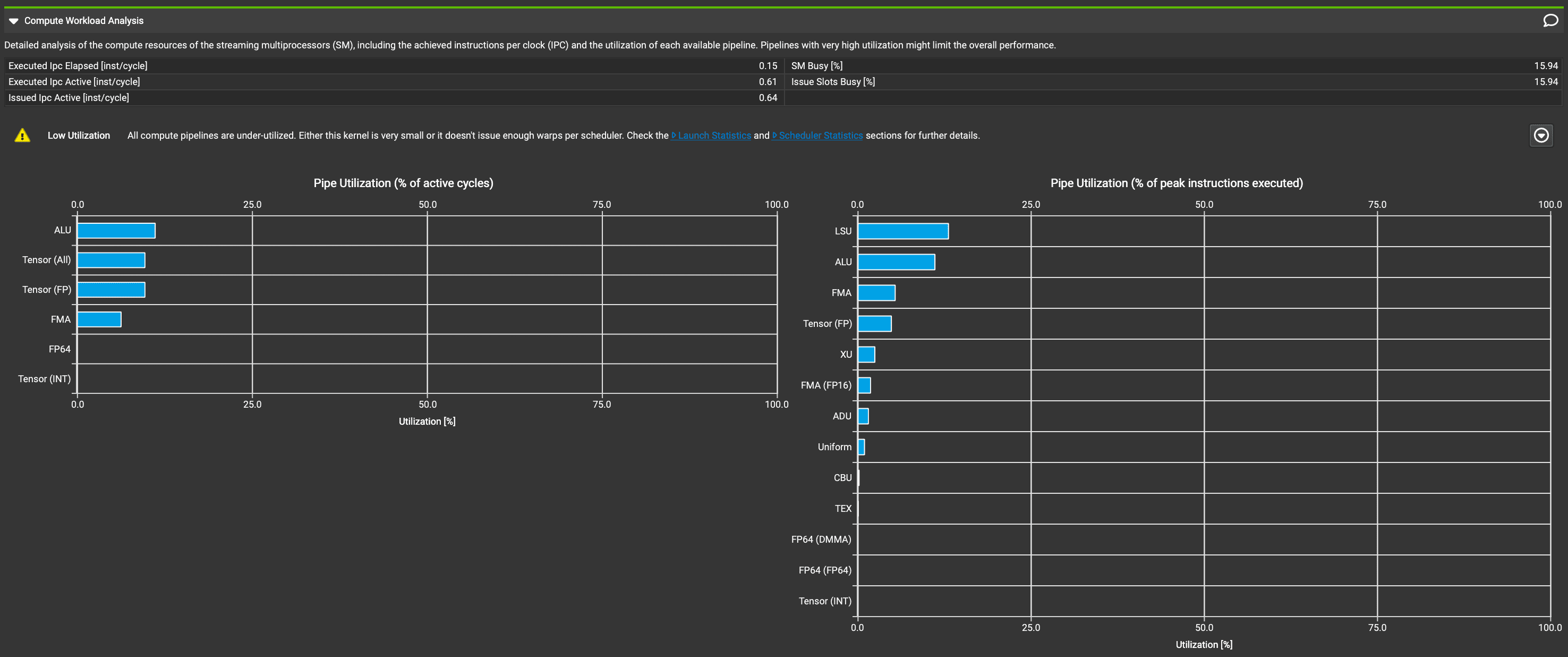
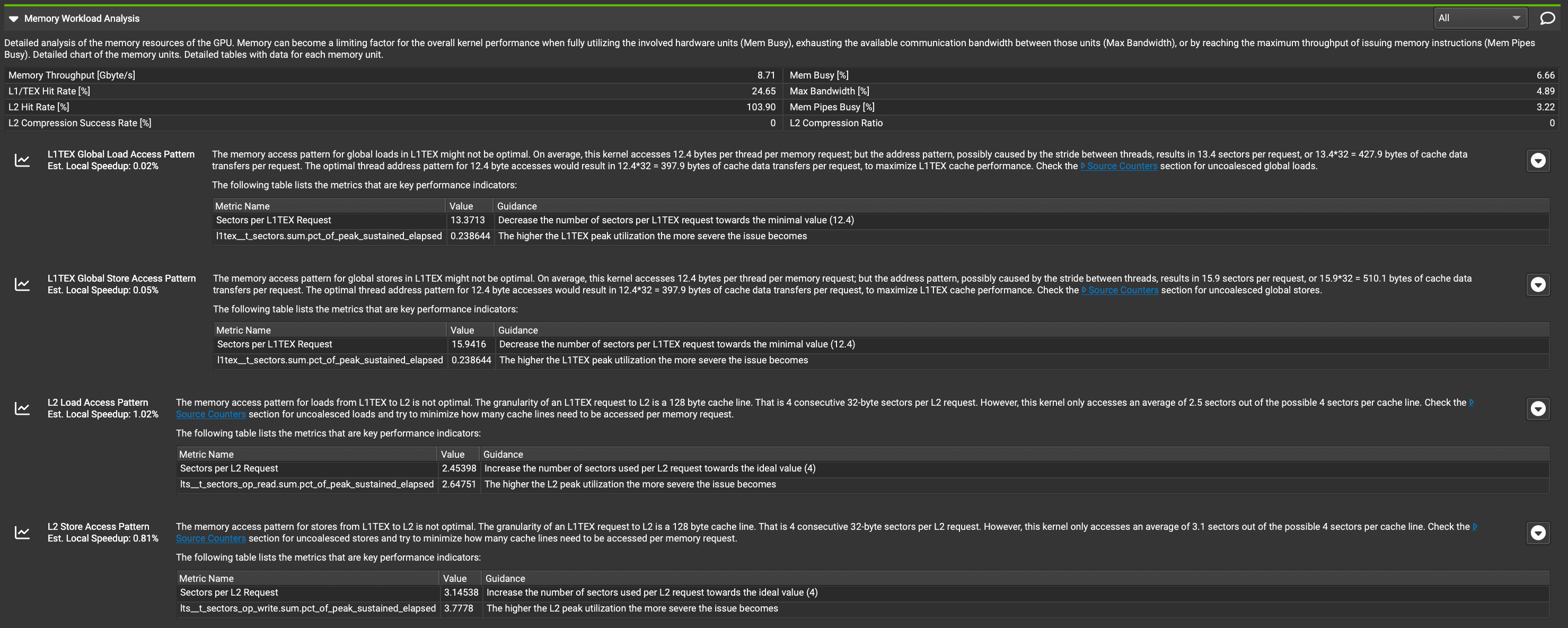
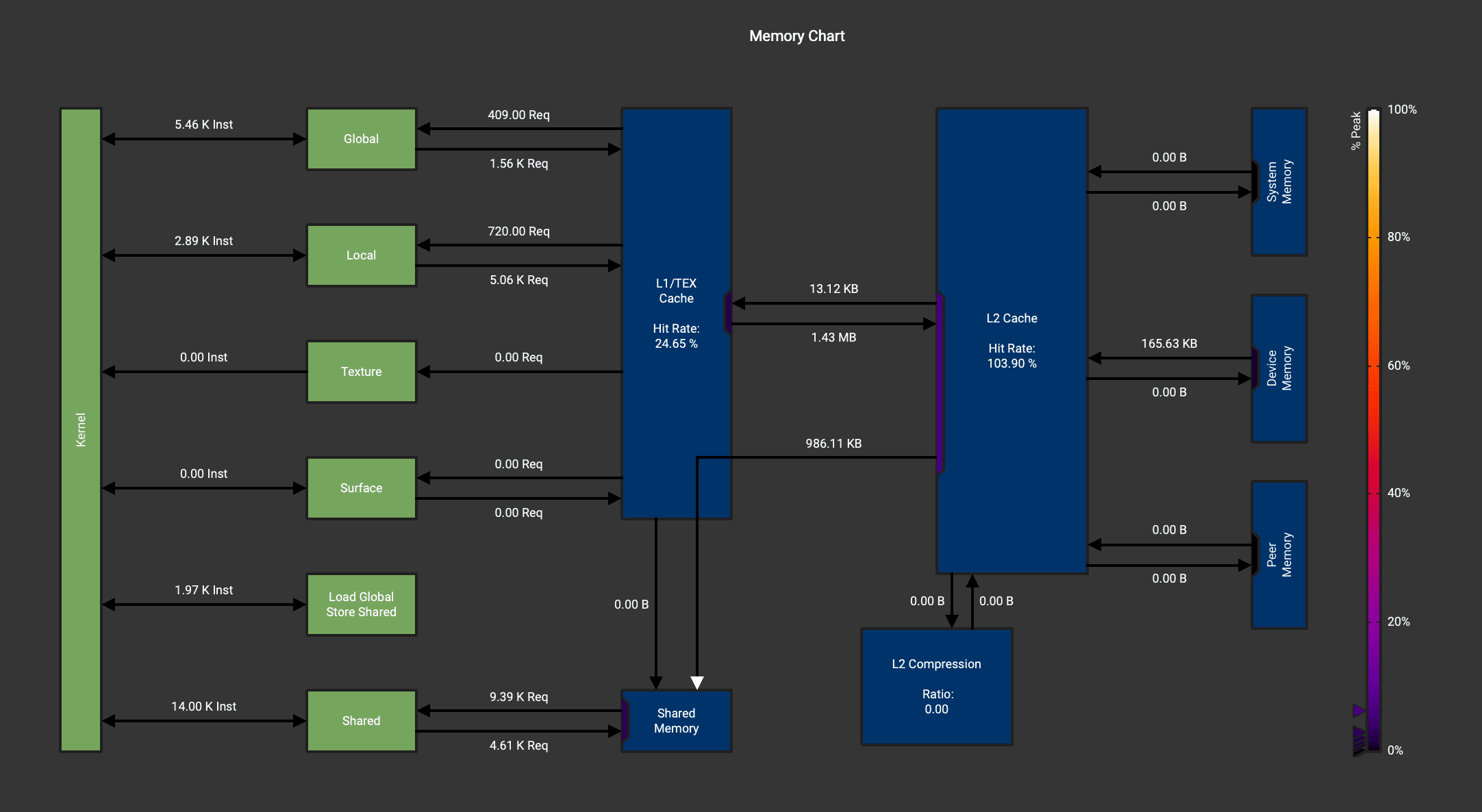

https://zhuanlan.zhihu.com/p/714731771


