Zhao Dongyu's Blog

A life which is unexamined is not worth living.

0%

WeightonlyGEMM:dequantize_s4_to_fp16x2代码解析

Posted on Edited on Views: 20
Symbols count in article: 8.9k Reading time ≈ 8 mins.

本文聚焦于AWQ的W4A16 (4-bit weight, 16-bit activation) CUDA kernel的反量化。

背景

在 ZZK大佬的文章 可能是讲的最清楚的WeightonlyGEMM博客 中学到很多知识

最近在学AWQ的量化，AWQ论文

其中我比较关注GPU的部分，其中数据排布这块很有意思：

于是到Who Says Elephants Can’t Run 这篇论文看了一下，WeightOnly GEMM 技术就是在这里提出的，其中权重反量化是这么操作的：

这个论文提出了一种 `IntToFloat 的巧妙的方式，可以大大提速反量化速度。

背景介绍结束，更详细的讲解可以直接看ZZK大佬的文章，接下来解释 dequantize_s4_to_fp16x2 代码。

代码

首先放出完整代码（80行）： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
__device__ uint4 dequantize_s4_to_fp16x2(uint32_t const& source) {
#if defined(__CUDA_ARCH__) && __CUDA_ARCH__ < 750
  assert(false);
#else
  uint4 result;

  uint32_t* h = reinterpret_cast<uint32_t*>(&result);
  uint32_t const i4s = reinterpret_cast<uint32_t const&>(source);

  // First, we extract the i4s and construct an intermediate fp16 number.
  static constexpr uint32_t immLut = (0xf0 & 0xcc) | 0xaa;
  static constexpr uint32_t BOTTOM_MASK = 0x000f000f;
  static constexpr uint32_t TOP_MASK = 0x00f000f0;
  static constexpr uint32_t I4s_TO_F16s_MAGIC_NUM = 0x64006400;

  // Note that the entire sequence only requires 1 shift instruction. This is
  // thanks to the register packing format and the fact that we force our
  // integers to be unsigned, and account for this in the fp16 subtractions. In
  // addition, I exploit the fact that sub and fma have the same throughput in
  // order to convert elt_23 and elt_67 to fp16 without having to shift them to
  // the bottom bits before hand.

  // Shift right by 8 to now consider elt_45 and elt_67. Issue first to hide RAW
  // dependency if we issue immediately before required.
  const uint32_t top_i4s = i4s >> 8;
  // Extract elt_01 - (i4s & 0x000f000f) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\\n"
               : "=r"(h[0])
               : "r"(i4s), "n"(BOTTOM_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));
  // Extract elt_23 (i4s & 0x00f000f0) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\\n"
               : "=r"(h[1])
               : "r"(i4s), "n"(TOP_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));
  // Extract elt_45 (top_i4s & 0x000f000f) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\\n"
               : "=r"(h[2])
               : "r"(top_i4s), "n"(BOTTOM_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));
  // Extract elt_67 (top_i4s & 0x00f000f0) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\\n"
               : "=r"(h[3])
               : "r"(top_i4s), "n"(TOP_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));

  // I use inline PTX below because I am not sure if the compiler will emit
  // float2half instructions if I use the half2 ctor. In this case, I chose
  // performance reliability over code readability.

  // This is the half2 {1032, 1032} represented as an integer.
  // static constexpr uint32_t FP16_TOP_MAGIC_NUM = 0x64086408;
  // Haotian: subtract {1024, 1024} instead, we do not need to map to [-8, 7]
  static constexpr uint32_t FP16_TOP_MAGIC_NUM = 0x64006400;
  // This is the half2 {1 / 16, 1 / 16} represented as an integer.
  static constexpr uint32_t ONE_SIXTEENTH = 0x2c002c00;
  // This is the half2 {-72, -72} represented as an integer.
  // static constexpr uint32_t NEG_72 = 0xd480d480;
  // Haotian: Let's use {-64, -64}.
  static constexpr uint32_t NEG_64 = 0xd400d400;

  // Finally, we construct the output numbers.
  // Convert elt_01
  asm volatile("sub.f16x2 %0, %1, %2;\\n"
               : "=r"(h[0])
               : "r"(h[0]), "r"(FP16_TOP_MAGIC_NUM));
  // Convert elt_23
  asm volatile("fma.rn.f16x2 %0, %1, %2, %3;\\n"
               : "=r"(h[1])
               : "r"(h[1]), "r"(ONE_SIXTEENTH), "r"(NEG_64));
  // Convert elt_45
  asm volatile("sub.f16x2 %0, %1, %2;\\n"
               : "=r"(h[2])
               : "r"(h[2]), "r"(FP16_TOP_MAGIC_NUM));
  // Convert elt_67
  asm volatile("fma.rn.f16x2 %0, %1, %2, %3;\\n"
               : "=r"(h[3])
               : "r"(h[3]), "r"(ONE_SIXTEENTH), "r"(NEG_64));

  return result;
#endif
}

代码解析

接下来逐句分析： 

1
__device__ uint4 dequantize_s4_to_fp16x2(uint32_t const& source)

这行代码定义了一个名为 dequantize_s4_to_fp16x2 的函数，这个函数是一个 CUDA 设备函数 (device)，它的输入是一个常量引用 uint32_t 类型的 source，返回值是 uint4 类型。

1
2
3
#if defined(__CUDA_ARCH__) && __CUDA_ARCH__ < 750
  assert(false);
#else

这段预处理指令检查 CUDA 架构版本是否小于 750。如果是，则触发断言错误，表明该代码不适用于 CUDA 750 以下的架构。否则，继续执行后面的代码。 比如这个函数里面用到了 lop3.b32 函数，可以在 这里 查到

Requires sm_50 or higher.
Qualifier .BoolOp requires sm_70 or higher.
1
2
3
4
uint4 result;

uint32_t* h = reinterpret_cast<uint32_t*>(&result);
uint32_t const i4s = reinterpret_cast<uint32_t const&>(source);

这里定义了一个 uint4 类型的变量 result。

接着将 result 的地址转换为 uint32_t* 类型的指针 h，以便后续的位操作。

然后将 source 重新解释为 uint32_t 类型并赋值给 i4s。

通过类型转换和指针操作，使得对这些整数的访问和操作更加便捷。

1
2
3
4
static constexpr uint32_t immLut = (0xf0 & 0xcc) | 0xaa;
static constexpr uint32_t BOTTOM_MASK = 0x000f000f;
static constexpr uint32_t TOP_MASK = 0x00f000f0;
static constexpr uint32_t I4s_TO_F16s_MAGIC_NUM = 0x64006400;

这里定义了一些用于位操作的常量：

  • immLut 是一个查找表的立即数。

  • BOTTOM_MASK 是用于提取较低位的掩码。

  • TOP_MASK 是用于提取较高位的掩码。

  • I4s_TO_F16s_MAGIC_NUM 是用于整数转换为半精度浮点数的魔数。

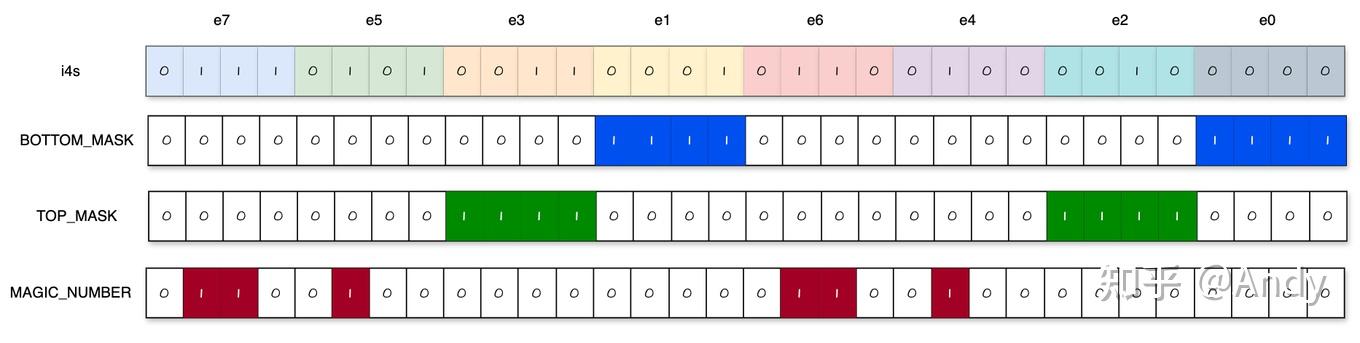
这几个数在内存中是这么表示的，后面用到的时候会仔细说，那时候会发现这几个数可真妙啊。

1
const uint32_t top_i4s = i4s >> 8;

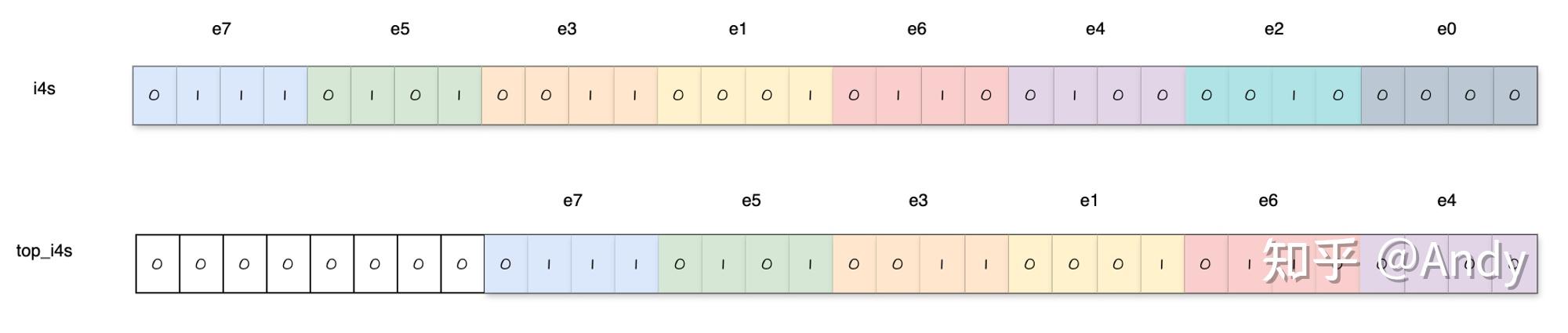
这里是将 i4s 向右移位8位，以便处理 elt_45 和 elt_67。暂时先不要管为什么这么做。 到这里，预备工作都做好了，接下来开始重头戏。

处理e0 e1元素

1
2
3
4
5
// Extract elt_01 - (i4s & 0x000f000f) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\\n"
               : "=r"(h[0])
               : "r"(i4s), "n"(BOTTOM_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));

使用内联 PTX 指令 lop3.b32 执行逻辑操作，将 i4s 的低位（BOTTOM_MASK 掩码）与 I4s_TO_F16s_MAGIC_NUM 结合并存储在 h[0] 中。

首先看一下 lop3.b32 执行了什么操作，这个 lop3.b32 是一种CUDA汇编指令，用于执行 三元逻辑运算。它利用查找表（immLut）来简化逻辑操作。这个函数可以在这里查到.

For a logical operation F(a, b, c) the value of immLut can be computed by applying the same operation to three predefined constant values as follows:

ta = 0xF0;
tb = 0xCC;
tc = 0xAA;

immLut = F(ta, tb, tc);

比如： 

1
2
3
4
5
6
7
8
9
10
11
If F = (a & b & c);
immLut = 0xF0 & 0xCC & 0xAA = 0x80

If F = (a | b | c);
immLut = 0xF0 | 0xCC | 0xAA = 0xFE

If F = (a & b & ~c);
immLut = 0xF0 & 0xCC & (~0xAA) = 0x40

If F = ((a & b | c) ^ a);
immLut = (0xF0 & 0xCC | 0xAA) ^ 0xF0 = 0x1A

现在我们可以看一下刚才定义的 immLut = (0xf0 & 0xcc) | 0xaa; 那我们得到的操作就是 (a & b) | c，也就是( i4s & BOTTOM_MASK) | I4s_TO_F16s_MAGIC_NUM.

这里先插一句，这个immLut设置的实在是太妙了！首先，abc这三个数可以形成一个 3 bit 的编码，可以表示 8 种状态，

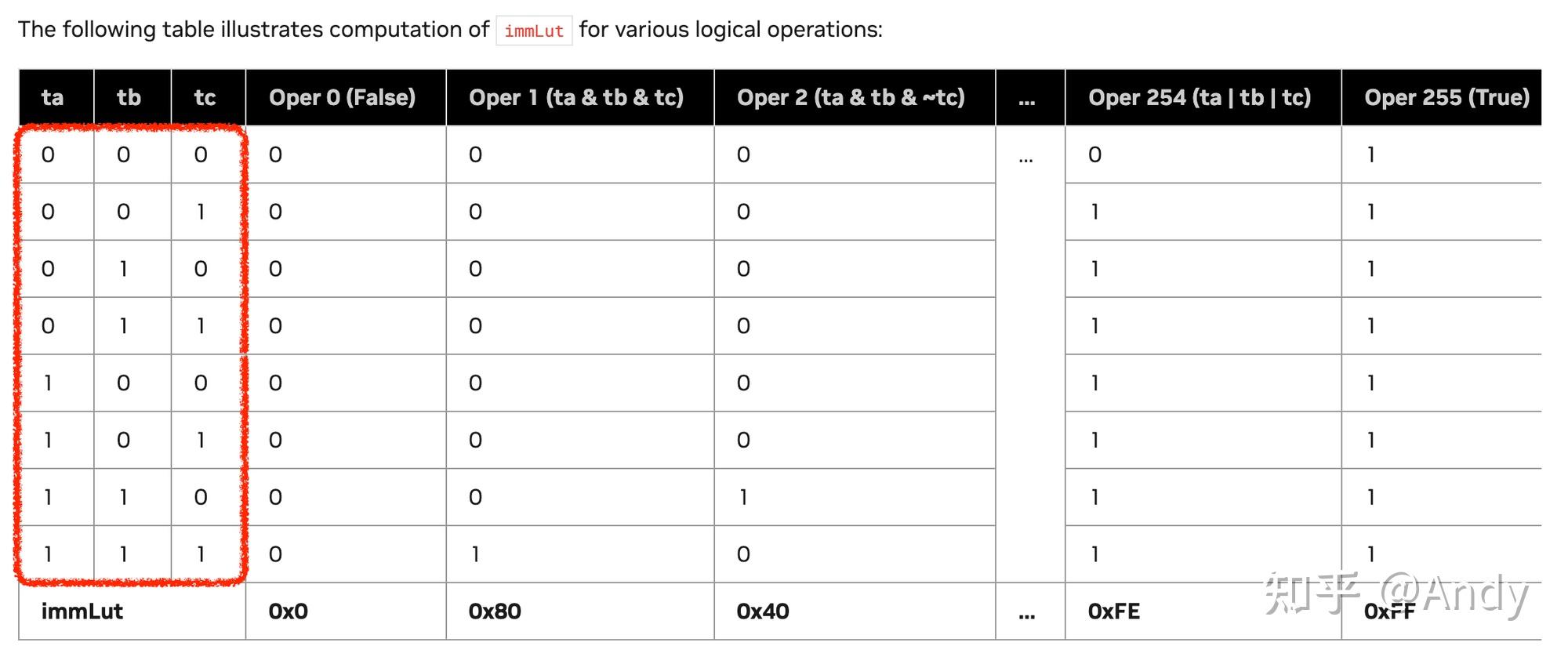
然后无论abc进行什么样的三元逻辑操作，得到的结果都是唯一的，这也就形成了immLut的表。实在是妙啊。

1
2
3
4
5
// Extract elt_01 - (i4s & 0x000f000f) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\\n"
               : "=r"(h[0])
               : "r"(i4s), "n"(BOTTOM_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));

然后结合具体数值看一下是怎么操作的：

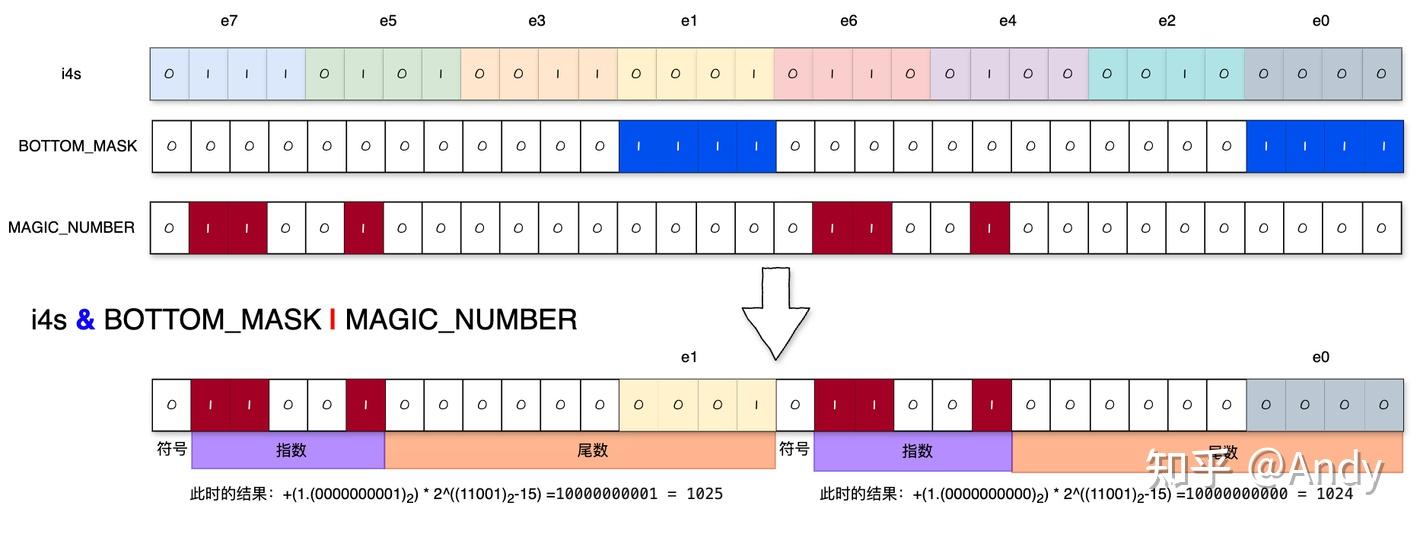
这一步操作是提取元素0和元素1的，这里设置元素0是0000，即 0，元素1是0001，即 1。

i4s与BOTTOM_MASK进行位与操作后，实际上就是把e0和e1筛选了出来，和I4s_TO_F16s_MAGIC_NUM进行位或操作后，是给指数位进行了赋值。

现在看这个 I4s_TO_F16s_MAGIC_NUM ，0x64006400，只看这个指数位部分是 11001，对应数字 25，fp16指数位的偏移量为 2**4−1=15, 那么偏移后指数为 25 - 15 = 10。

以e1为例，

尾数位是0.0000000001，加上1，那就是1.0000000001。

指数位是10，所以结果是1.00000001*2^10 = 10000000001。也就是小数点向后移动10位。

这个结果的十进制是 1025。

这时候就可以理解这个 I4s_TO_F16s_MAGIC_NUM 为什么这么设置了——原来的数值类型是int4，肯定是整数，那么问题的关键就是要把尾数放大到一定程度，使新的数值是整数。那么，显而易见，要把小数点向右移动10位（因为尾数位有10位），也就反推出了magic number的具体数值，妙啊。

显然，此时的结果并不正确，因为加了1并且右移了10位，也就是加了1024，所以我们要把结果减去1024才可以，所以还需要进行这一步操作：

1
2
3
4
// Convert elt_01
  asm volatile("sub.f16x2 %0, %1, %2;\\n"
               : "=r"(h[0])
               : "r"(h[0]), "r"(FP16_TOP_MAGIC_NUM));

其中，FP16_TOP_MAGIC_NUM = 0x64006400;

这句代码实现了减1024这个操作，于是最终得到fp16格式的e1=1， e0=0，数据无误。

需要注意的是，FP16_TOP_MAGIC_NUM = 0x64006400;这个数代表的其实是fp16格式的 1024。

我最开始在这里感到疑惑，心想为什么要减这么一个数，这也不是1024啊，直到后来意识到现在是在做fp16的减法，那么当然也要是fp16的格式。

ok，到现在为止，最难的部分就理解完了。接下来看一下别的情况：

处理e2 e3元素

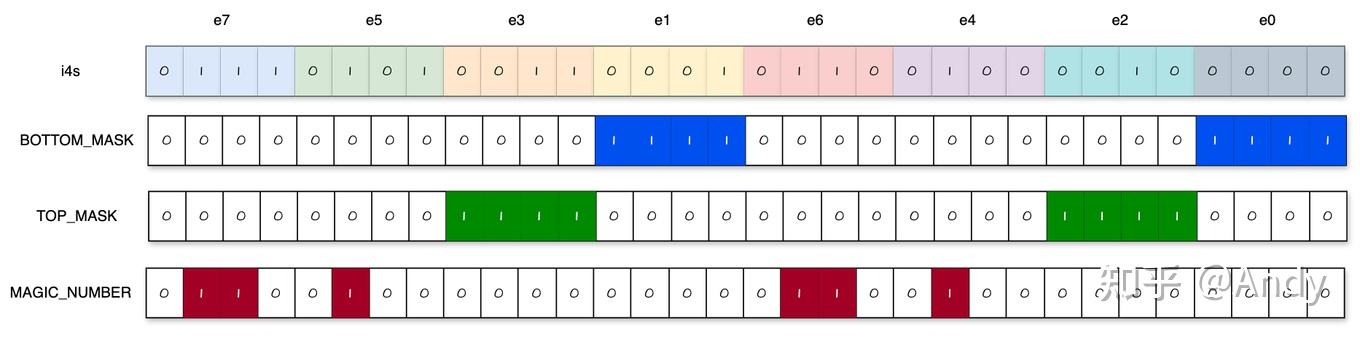
对于e2、e3而言，这时候就不能用 BOTTOM_MASK 来进行位与操作了，应该改为 TOP_MASK

1
2
3
4
5
// Extract elt_23 (i4s & 0x00f000f0) | 0x64006400
  asm volatile("lop3.b32 %0, %1, %2, %3, %4;\\n"
               : "=r"(h[1])
               : "r"(i4s), "n"(TOP_MASK), "n"(I4s_TO_F16s_MAGIC_NUM),
                 "n"(immLut));

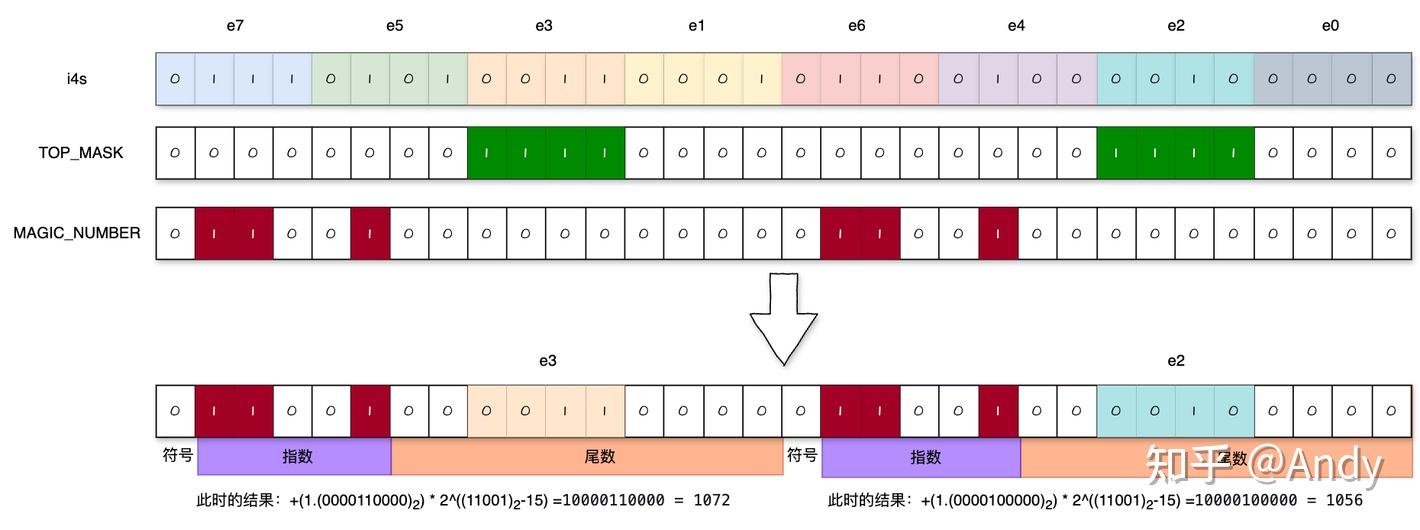
如果减去1024，呢么得到e3=48，e2=32，这和刚才不太一样，事情变得不太简单。

问题在哪？以e3为例，这时候小数点右移10位意味着把e3乘了2^4=16，所以当前的结果是1024 + X * 16。

所以针对e2、e3的下一步操作稍有不同：

1
2
3
4
// Convert elt_23
  asm volatile("fma.rn.f16x2 %0, %1, %2, %3;\\n"
               : "=r"(h[1])
               : "r"(h[1]), "r"(ONE_SIXTEENTH), "r"(NEG_64));

其中，ONE_SIXTEENTH = 0x2c002c00; NEG_64 = 0xd400d400;

这是做了什么操作？可以理解为

(1024 + X * 16) * (1/16) - 64 = X

ok，到现在为止，e0e1e2e3都搞定了，最后看一下e4e5，

处理e4 e5元素

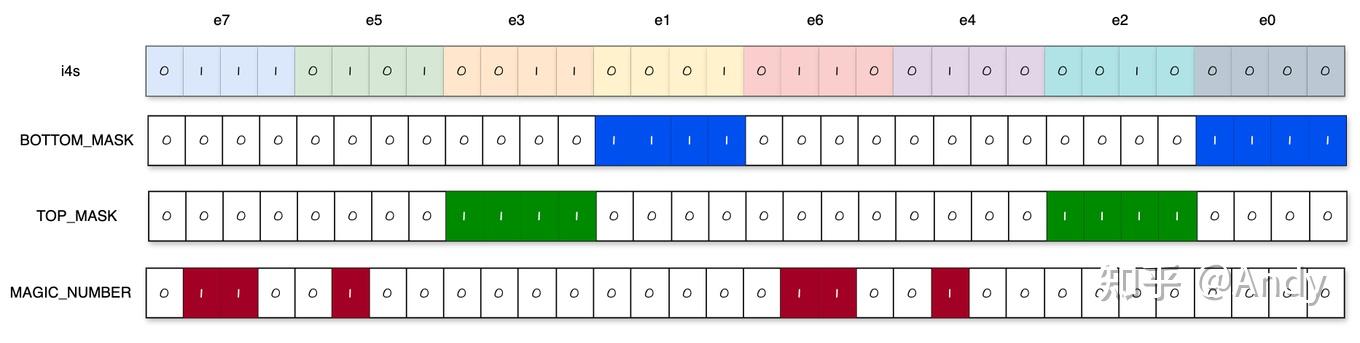
e4 e5元素怎么提取呢？可以先认真思考一下。

我最开始的想法是，针对e4 e5的位置，再写一个mask进行位与操作不就好了，然后和前面做一样的操作。

但是这样是不可行的，以e5为例，这时候e5在16位的高8位，与fp16的指数位有冲突。

那么，处理方式就很简单了，文章最开始的时候提到过这个操作：

1
const uint32_t top_i4s = i4s >> 8;

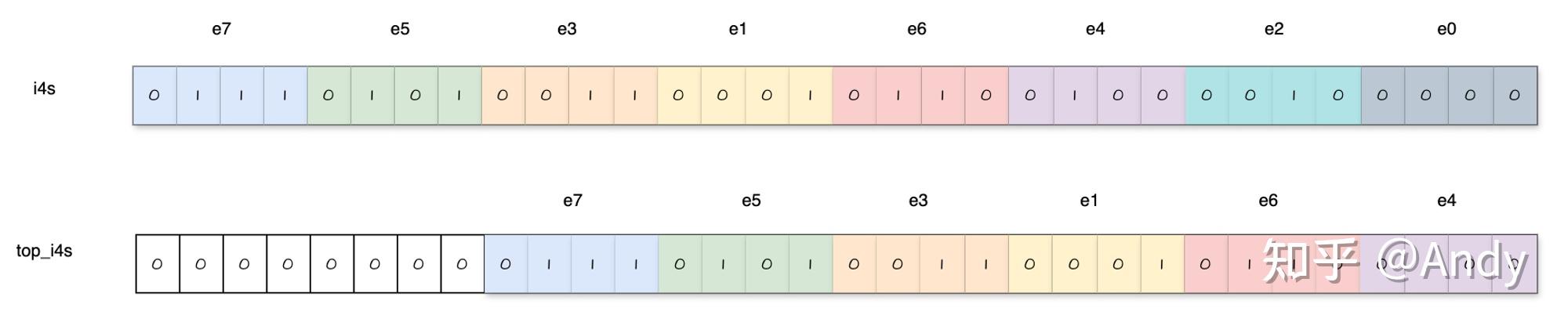
这里是将 i4s 向右移位8位，以便处理 elt_45 和 elt_67。

这样一来，就可以按照e0 e1的方式处理e4 e5了。

ok，到现在为止，e0 e1 e2 e3 e4 e5都搞定了，有了前面的基础，e6 e7理解起来就很简单，这里不做过多赘述。

整个代码实现到这里也就讲完了。

写在最后

最后，补充几点

  • 对于e2e3而言，为什么不像e5e6那样，向右移动8位，然后做e0e1相同的操作？

    这样的操作从逻辑上确实更好理解，也避免了后面的乘1/16的操作，看上去似乎更简单。

    但是要明白一点，e5e6那样，向右移动8位，是不得不这么做。

    为了性能，e2e3没必要额外增加一个移位操作。所以关键点只剩一个：fma.rn.f16x2指令和sub.f16x2指令的区别，如果 移位+sub指令 快于 fma.rn指令，那就是赚的。代码中的注释标明了这一点：

      In addition, I exploit the fact that sub and fma have the same throughput in order to convert elt_23 and elt_67 to fp16 without having to shift them to the bottom bits before hand.

    sub（减法）和 fma（乘法累加）具有相同的吞吐量，这意味着它们的性能相当。

  • 为什么要做interleave？

    本文缘起就是因为研究这个权重排布

    前文中一直没有提这件事——为什么权重是interleave排布？

    按照zzk大佬的观点，对于Int8来说，本来就是不需要Interleave的，但是Int4快速转换不能使用PRMT指令，需要通过一些trick，进而需要这个交错权重的格式

    也就是说，int8快速反量化中，使用了PRMT指令，这个指令的操作粒度是字节byte；而int4是sub-byte，不足一个字节；因此，原来在INT8快速反量化的那一套无法直接用在int4上。

    所以针对int4，使用指令LOP3来替代PRMT，从而完成了int4快速反量化到fp16的核心逻辑。通过交错权重，可以减少shift指令，提高性能。关于这一点，我认为[LLM推理优化]🔥WINT8/4-(03): LOP3指令详解及INT4转FP16/BF16分析 讲解的比较详细。

Thanks for your support.
0 comments
Anonymous
Markdown is supported

Be the first person to leave a comment!